Виет теоремасы

Сабақ №25

Сынып:8

Пән: алгебра

Тақырыбы: Виет теоремасы

Типі: жаңа білімді меңгеру

Мақсаты:

Білімділік: Виет теоремасының дәлелдеуін көрсетіп, есептер шығарғанда

пайдалануға жаттықтыру

Дамытушылық: ауызша, жазбаша есептеу алгоритмін орындау, квадрат

теңдеу түбірлері арқылы теңдеу құру дағдыларын дамыту;

Тәрбиелік: оқушылардың білімдерін дамыта отырып пәнге деген қызығушылықтарын арттыру және ұйымшылдыққа тәрбиелеу.

Сабақ түрі: практикалық

Сабақ көрнекілігі: интерактивті тақта, слайдтар, оқулық.

Сабақ барысы:

VII. Ұйымдастыру.

6) оқушыларды түгендеу;

7) оқушылардың сабаққа дайындығын тексеру;

8) сабаққа назарын аудару;

9) сабақтың мақсаты мен міндетін баяндау;

VIII. Жаңа білімді меңгеруге дайындық.

1) квадрат теңдеудің түрлері: толық , толымсыз, келтірілген

,

2) толық квадрат теңдеудің түбірлерін табу формуласы:

, ,

3) толық квадрат теңдеуді келтірілген квадрат теңдеуге қалай келтіреміз?

IX. Жаңа білімді меңгеру

1) квадрат теңдеудің түбірлерін қосайық

2) квадрат теңдеудің түбірлерін көбейтейік

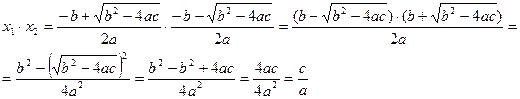
3) екендігін көріп тұрмыз.Ендеше мынадай теорема шығады.

Теорема: Келтірілген квадрат теңдеудің түбірлерінің қосындысы қарама-қарсы таңбамен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең.

Егер келтірілген квадрат теңдеудегі белгілесек, онда

, .

Осы теореманы Виет теоремасы деп аталады.

D=0, Виет торемасын қолдануға болады ма?

теңдеуінің D=0 жағдайында өзара тең екі түбірі бар және олардың әрқайсысы -ге тең.

Бұл екі түбірді және формуласынан деп ұйғарып, аламыз. D=0 жағдайы үшін де Виет теоремасы дұрыс. Расында

Виет теоремасына кері теорема да дұрыс.

Теорема. (Виет теоремасына кері теорема). Егер екі санның қосындысы –р-ға, ал олардың көбейтіндісі q-ға тең болса, онда ол сандар теңдеуінің түбірлері болады.

X. Жаңа материалды меңгергенін тексеру.

Оқулықпен жұмыс: №147, №148, №150

XI. Қорытынды .

Виет теоремасы	Кері теорема
Егер теңдеуінің х1 және х2 сандары түбірі болса, онда х1+х2=-р, х1*х2=q болады.	Қандай да бір сан берілсін. Олар: х1, х2, р, q болсын. Онда теңдеуінің х1, х2 сандары түбірі болады.

XII. Үй жұмысы. №149, №151