Цель: рассмотреть графики и свойства функций у = tg х, у = ctg х.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант I
1. Как построить график функции:
![]()
2. Постройте график функции:
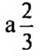
Вариант 2
1. Как построить график функции:
![]()
2. Постройте график функции:
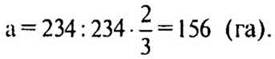
III. Изучение нового материала
Рассмотрим две оставшиеся тригонометрические функции – тангенс и котангенс.
1. Функция у = tg x
Остановимся на графиках функций тангенса и котангенса. Сначала обсудим построение графика функции у = tg х на промежутке ![]() Такое построение аналогично построению графика функции у = sin х, описанному ранее. При этом значение функции тангенса в точке находится с помощью линии тангенсов (см. рисунок).
Такое построение аналогично построению графика функции у = sin х, описанному ранее. При этом значение функции тангенса в точке находится с помощью линии тангенсов (см. рисунок).
Учитывая периодичность функции тангенса, получаем ее график на всей области определения параллельными переносами вдоль оси абсцисс (вправо и влево) уже построенного графика на π, 2π и т. д. График функции тангенса называют тангенсоидой.
Приведем основные свойства функции у = tg х:
1. Область определения – множество всех действительных чисел, за исключением чисел вида ![]()
2. Функция нечетная (т. е. у(-х) = -y(x)), и ее график симметричен относительно начала координат.
3. Функция возрастает на промежутках вида ![]() где к ∈ Z.
где к ∈ Z.
4. Функция не ограничена.
5. Функция не имеет наименьшего и наибольшего значений.
6. Функция непрерывная.
7. Область значений Е(у) = (-∞; +∞).
8. Функция периодическая с наименьшим положительным периодом Т = π, т. е. у(х + пk) = у(х).
9. График функции имеет вертикальные асимптоты ![]()
Пример 1
Установим четность или нечетность функции:
Легко проверить, что для функций а, б область определения – симметричное множество. Исследуем эти функции на четность или нечетность. Для этого найдем у(-х) и сравним значения у(х) и y(-x).
а) Получим: ![]()
![]() Так как выполнено равенство y(-x) = у(х), то функция у(х) по определению четная.
Так как выполнено равенство y(-x) = у(х), то функция у(х) по определению четная.
б) Имеем: ![]()
![]()
Так как выполнено равенство y(-x) = -у(х), то функция у(х) по определению нечетная.
в) Область определения данной функции – несимметричное множество. Например, функция определена в точке х = π/4 и не определена в симметричной точке х = -π/4. Поэтому данная функция определенной четности не имеет.
Пример 2
Найдем основной период функции ![]()
Данная функция у(х) представляет собой алгебраическую сумму трех тригонометрических функций, периоды которых равны: T1 = 2π, ![]() Запишем эти числа в виде дробей с одинаковыми знаменателями
Запишем эти числа в виде дробей с одинаковыми знаменателями ![]() Наименьшее общее кратное коэффициентов НОК (6; 2; 3). Поэтому основной период данной функции
Наименьшее общее кратное коэффициентов НОК (6; 2; 3). Поэтому основной период данной функции ![]()
Пример 3
Построим график функции ![]()
Учтем правила преобразования графиков функции. В соответствии с ними график функции ![]() получается смещением графика функции у = tg х на π/4 единиц вправо вдоль оси абсцисс и его растяжением в 2 раза вдоль оси ординат.
получается смещением графика функции у = tg х на π/4 единиц вправо вдоль оси абсцисс и его растяжением в 2 раза вдоль оси ординат.
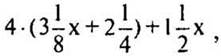
Пример 4
Построим график функции 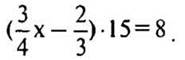
Используя определение и свойства модуля, в аргументе функции раскроем знаки модуля, рассмотрев три случая. Если х < 0, то имеем: ![]() При 0 ≤ x ≤ π/4 имеем:
При 0 ≤ x ≤ π/4 имеем: ![]() Для х > π/4 имеем:
Для х > π/4 имеем: ![]() Далее остается построить три части данного графика. При х < 0 строим прямую у = -1. Для 0 ≤ x ≤ π/4 строим тангенсоиду
Далее остается построить три части данного графика. При х < 0 строим прямую у = -1. Для 0 ≤ x ≤ π/4 строим тангенсоиду ![]() Этот график получается смещением графика функции у = tg х на π/8 вправо вдоль оси абсцисс и сжатием в два раза вдоль этой оси. При х > π/4 строим прямую у = 1.
Этот график получается смещением графика функции у = tg х на π/8 вправо вдоль оси абсцисс и сжатием в два раза вдоль этой оси. При х > π/4 строим прямую у = 1.
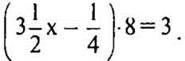
2. Функция у = ctg x
Аналогично графику функции у = tg х или с помощью формулы приведения ![]() строится график функции у = ctg x.
строится график функции у = ctg x.
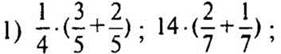
Перечислим основные свойства функции у = ctg x:
1. Область определения – множество всех действительных чисел, за исключением чисел вида х = пk, к ∈ Z.
2. Функция нечетная (т. е. у(-х) = -y(x)), и ее график симметричен относительно начала координат.
3. Функция убывает на промежутках вида (пk; п + пk), к ∈ Z.
4. Функция не ограничена.
5. Функция не имеет наименьшего и наибольшего значений.
6. Функция непрерывная.
7. Область значений Е(у) = (-∞; +∞).
8. Функция периодическая с наименьшим положительным периодом Т = п, т. е. у(х + пk) = у(x).
9. График функции имеет вертикальные асимптоты х = пk.
Пример 5
Найдем область определения и область значений функции ![]()
Очевидно, что область определения функции y(x) совпадает с областью определения функции z = ctg х, т. е. область определения – множество всех действительных чисел, кроме чисел вида х = nk, k ∈ Z.
Функция y(х) сложная. Поэтому запишем ее в виде ![]() Координаты вершины параболы y(z): zB = 1 иyв = 2 – 4 + 5 = 3. Тогда область значений данной функции Е(у) = [3; +∞).
Координаты вершины параболы y(z): zB = 1 иyв = 2 – 4 + 5 = 3. Тогда область значений данной функции Е(у) = [3; +∞).
Пример 6
Построим график уравнения ![]()
Из формы записи уравнения следует, что ctg(x + у) = 0 и sin х ≠ 0, cos у ≠ 0. Из уравнения ctg(x + у) = 0 находим ![]() (где k ∈ Z) и
(где k ∈ Z) и ![]() Построим семейство этих прямых. Теперь учтем ограничение sin х ≠ 0, откуда х ≠ πm (где m ∈ Z). Удалим эти точки из построенных прямых (пустые точки).
Построим семейство этих прямых. Теперь учтем ограничение sin х ≠ 0, откуда х ≠ πm (где m ∈ Z). Удалим эти точки из построенных прямых (пустые точки).
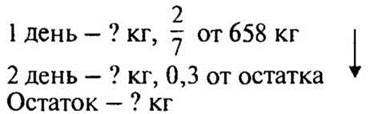
Рассмотрим второе ограничение – cos у ≠ 0. Подставим в него величину ![]() и получим:
и получим: ![]() или по формуле приведения sin х ≠ 0. Таким образом, второе ограничение свелось к первому (уже учтенному).
или по формуле приведения sin х ≠ 0. Таким образом, второе ограничение свелось к первому (уже учтенному).
Пример 7
Построим множество точек, для которых выполнено неравенство ctg(y – x) ≥ 0.
Прежде всего решим данное неравенство. Функция котангенса принимает неотрицательные значения для углов, расположенных в первой четверти, т. е. 0 < у – х ≤π/2. Учитывая периодичность функции котангенса, получим: ![]() где k ∈ Z. Ко всем частям этого двойного неравенства прибавим x и найдем
где k ∈ Z. Ко всем частям этого двойного неравенства прибавим x и найдем ![]() На координатной плоскости изобразим множество таких точек (показаны штриховкой). Стрелки указывают, что такие точки решением не являются.
На координатной плоскости изобразим множество таких точек (показаны штриховкой). Стрелки указывают, что такие точки решением не являются.
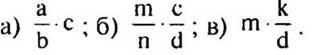
IV. Контрольные вопросы (фронтальный опрос)
1. Основные свойства и график функции у = tg х.
2. Функция у = ctg х, ее свойства и график.
V. Задание на уроках
§ 14, № 1; 3 (а, б); 5; 6 (в, г); 7 (а, в); 8; 10 (а, б); 11; 13 (а); 14 (б); 15 (a).
VI. Задание на дом
§ 14, № 2; 3 (в, г); 4; 6 (а, б); 7 (б, г); 9; 10 (в, г); 12; 13 (б); 14 (а); 15 (6).
VII. Творческие задания
1. Определите четность или нечетность функции:
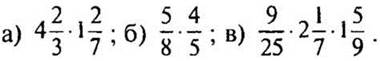
Ответы: а, б) нечетные; в, г) четные; д-з) определенной четности не имеют.
2. Постройте график функции, уравнения или неравенства:
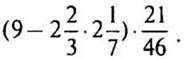
VIII. Подведение итогов уроков














