Цели: детальнее рассмотреть функции у = sin х и у = cos х, их свойства и графики; обсудить периодичность этих функций.
Ход уроков
I. Сообщение темы и целей уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Вычислите ![]()
2. Упростите выражение:
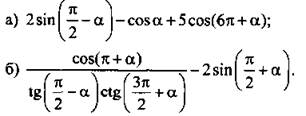
Вариант 2
1. Вычислите ![]()
2. Упростите выражение:
![]()
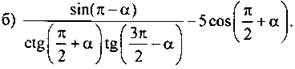
III. Изучение нового материала
Из ранее изученного нам известны многие свойства двух основных тригонометрических функций – синуса и косинуса. Рассмотрим графики этих функций и на их основе детализируем такие свойства.
1. Функция y = sin x, ее свойства и график
Обсудим построение графиков функций синуса и косинуса. Сначала построим график функции синуса на отрезке [0; 2π]. Отметим на оси ординат точки (0; -1) и (0; 1), на оси абсцисс – точку (2π; 0). Разделим отрезок [0; 2π] и единичную окружность на 8 равных частей (учтите, что длина отрезка [0; 2π] равна 2π ≈ 6,28). Каждая такая часть равна π/4. Для построения точки графика с абсциссой t используем определение синуса. Отметим точку Рt на единичной окружности и проведем через Рt прямую, параллельную оси абсцисс. Точка пересечения этой прямой и прямой х = t искомая, так как ее ордината совпадает с ординатой точки Рt и по определению sin t равен ординате точки Рt.
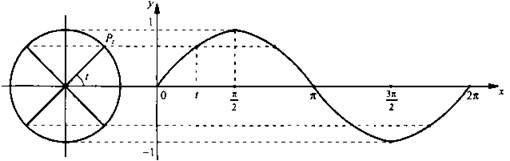
На рисунке приведено построение восьми точек графика. Соединяя их плавной кривой, получаем эскиз графика синуса на отрезке [0; 2π]. Для построения графика функции вне этого отрезка учтем периодичность функции синуса, т. е. sin (х + 2πn) = sin х (где n – произвольное целое число). Поэтому во всех точках х0 + 2пn (где 0 < x0 < 2π) значения синуса совпадают. Следовательно, график синуса на всей прямой получается из построенного графика с помощью параллельных переносов его вдоль оси абсцисс (вправо и влево) на 2π, 4π, 6π и т. д. График функции синуса называется синусоидой. Отрезок [-1; 1] оси ординат, с помощью которого находили значения синуса, иногда называют линией синусов.
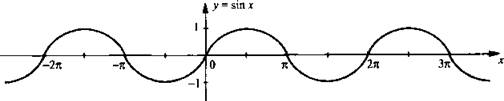
Используя построенный график, приведем основные свойства функции у = sin х:
1. Область определения D(y) = (-∞; +∞).
2. Функция нечетная (т. е. у(-x) = -e(x))> и ее график симметричен относительно начала координат.
3. Функция возрастает на отрезках вида ![]() и убывает на отрезках вида
и убывает на отрезках вида ![]() где k ∈ Z.
где k ∈ Z.
4. Функция ограничена, т. е. -1 ≤ у(х) ≤ 1.
5. Наименьшее значение функции yнаим = -1 (достигается в точках вида ![]() ) и наибольшее значение унаиб = 1 (достигается в точках вида
) и наибольшее значение унаиб = 1 (достигается в точках вида ![]() ).
).
6. Функция непрерывная.
7. Область значений Е(у) = [-1; 1].
8. Функция периодическая с наименьшим положительным периодом Т = 2п, т. е. у(х + 2пk) = y(x).
Рассмотрим некоторые примеры.
Пример 1
Найдем наименьшее и наибольшее значения функции: ![]()
а) В силу ограниченности функции у = sin х имеем неравенство -1 ≤ sin x ≤ 1. Умножим все части этого неравенства на положительное число 3 и получим неравенство того же знака -3 ≤ 3sin x ≤ 3. Вычтем их всех частей число 1: -4 ≤ 3sin х – 1 ≤ 2. Таким образом,yнаим = -4 и yнаиб = 2.
б) Используем основное тригонометрическое тождество (1) и в данной функции перейдем к величине sin х. Получим: ![]() Введем вспомогательную величину z = sin х, причем -1 ≤ z ≤ 1. Тогда необходимо найти наибольшее и наименьшее значения квадратичной функции
Введем вспомогательную величину z = sin х, причем -1 ≤ z ≤ 1. Тогда необходимо найти наибольшее и наименьшее значения квадратичной функции ![]() на отрезке [-1; 1].
на отрезке [-1; 1].
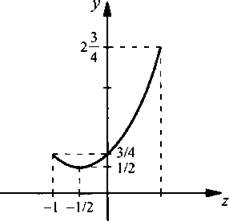
Графиком этой функции является парабола, направленная ветвями вверх (см. рисунок), вершина которой имеет координаты zB = -1/2 и 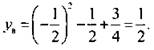 В этой точке функция имеет наименьшее значение. Наибольшее значение функция имеет в точке z = 1, и оно равно
В этой точке функция имеет наименьшее значение. Наибольшее значение функция имеет в точке z = 1, и оно равно ![]() Итак, получили:
Итак, получили: ![]() Поэтому
Поэтому ![]()
Пример 2
Построим график функции ![]()
Такой график получается из графика функции у = х смещением на π/6 влево вдоль оси абсцисс и растяжением в 2 раза вдоль оси ординат.
Пример 3
Построим график функции 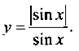
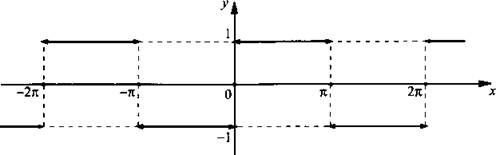
Раскроем знак модуля и получим 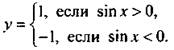 При sin х = 0 (т. е. х = пn, где n- любое целое число) данная функция не определена.
При sin х = 0 (т. е. х = пn, где n- любое целое число) данная функция не определена.
2. Функция у = cos x, ее свойства и график
Для построения графика функции косинуса учтем формулу приведения ![]() Поэтому значение косинуса в любой точке x0 равно значению синуса в точке
Поэтому значение косинуса в любой точке x0 равно значению синуса в точке ![]() Тогда график косинуса получается из графика синуса с помощью параллельного переноса на единиц влево вдоль оси абсцисс. Поэтому график функции у = cos х также является синусоидой.
Тогда график косинуса получается из графика синуса с помощью параллельного переноса на единиц влево вдоль оси абсцисс. Поэтому график функции у = cos х также является синусоидой.
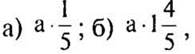
Перечислим основные свойства функции у = cos x:
1. Область определения D(y) = (-∞; +∞).
2. Функция четная (т. е. y(-х) = y(х)), и ее график симметричен относительно оси ординат.
3. Функция возрастает на отрезках вида [-π + 2πk; 2πk] и убывает на отрезках вида [2πk; π + 2πk], где k ∈ Z.
4. Функция ограничена, т. е. -1 ≤ y(х) ≤ 1.
5. Наименьшее значение функции унаим = -1 (достигается в точках вида х = π + 2пk) и наибольшее значение унаиб = 1 (достигается в точках вида х = 2пk).
6. Функция непрерывная.
7. Область значений Е(у) = [-1; 1].
8. Функция периодическая с наименьшим положительным периодом Т= 2п, т. е. у(х + 2пk) = у(х).
Рассмотрим наиболее типичные примеры.
Пример 4
Найдем область определения и область значений функции:
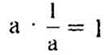
а) Для данной функции х может принимать любые значения, поэтому D(y) = R. Теперь найдем область значений функции. Так как -1 ≤ sin|x| ≤ 1, то умножим все члены этого неравенства на 3 и получим – 3 ≤ 3sin|x| ≤ 3 или -3 ≤ у ≤ 3, т. е. Е(у) = [-3; 3].
б) Аргумент данной функции существует при условии х2 – 2х ≥ 0. Решение этого неравенства х ∈ (-∞; 0]U[2; ∞), что и является областью определения функции у(х). Итак, D(y) = (-∞; 0]U[2; ∞). При изменении х в этих пределах величина ![]() меняется от 0 до ∞. Поэтому -1 ≤ cos z ≤ 1, тогда 2 ≥ -2cos z ≥ -2, или
меняется от 0 до ∞. Поэтому -1 ≤ cos z ≤ 1, тогда 2 ≥ -2cos z ≥ -2, или ![]() или -2 ≤ у ≤ 2, т. е. Е(у) = [-2; 2].
или -2 ≤ у ≤ 2, т. е. Е(у) = [-2; 2].
в) Аргумент этой функции существует при условии х ≠ 0 и D(y) = (-∞; 0)U(0; ∞). При изменении х в таких пределах величина z = 1/x изменяется в промежутках (-∞; 0)U(0; ∞). Тогда ![]() Поэтому Е(у) = [-5; 5].
Поэтому Е(у) = [-5; 5].
г) Промежуточный аргумент ![]() этой функции определен при всех значениях х, поэтому D(y) = R. Найдем промежуток, в котором меняется z. Запишем неравенство между средним арифметическим и средним геометрическим двух чисел – 1 и х2. Получим:
этой функции определен при всех значениях х, поэтому D(y) = R. Найдем промежуток, в котором меняется z. Запишем неравенство между средним арифметическим и средним геометрическим двух чисел – 1 и х2. Получим: ![]() Разделим обе части неравенства на положительное выражение 1 + x2 (при этом знак неравенства сохраняется)
Разделим обе части неравенства на положительное выражение 1 + x2 (при этом знак неравенства сохраняется) ![]() откуда
откуда ![]() т. е.
т. е. ![]() При изменении z в указанных пределах, как видно из единичной окружности, 0 ≤ cos z ≤ 1. Тогда 0 ≥ -4cos z ≥ -4 или -4 ≤ у ≤ 0. Поэтому Е(у) = [-4; 0].
При изменении z в указанных пределах, как видно из единичной окружности, 0 ≤ cos z ≤ 1. Тогда 0 ≥ -4cos z ≥ -4 или -4 ≤ у ≤ 0. Поэтому Е(у) = [-4; 0].
Заметим, что во всех пунктах а – г рассматривались сложные функции. Для того чтобы найти значение тригонометрической функции, необходимо было сначала найти значение промежуточного аргумента. Этот аргумент, в свою очередь, являлся функцией аргумента х. В пункте а промежуточным аргументом была функция z = |х|, в пункте б – ![]() в пункте в –
в пункте в – ![]() и в пункте г –
и в пункте г – ![]()
Пример 5
Установим четность или нечетность функции:
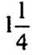
Для функций а-в область определения D(y) = R – симметричное множество. Для этих функций найдем у(-х).
а) ![]() Так как выполнено равенство y(-x) = -у(х), то данная функция по определению нечетная.
Так как выполнено равенство y(-x) = -у(х), то данная функция по определению нечетная.
б) ![]() Так как выполнено равенство y(-x) = у(х), то данная функция по определению четная.
Так как выполнено равенство y(-x) = у(х), то данная функция по определению четная.
в) ![]() Видно, что равенство y(-х) = -y(х) не выполняется, так как перед числом 1 один и тот же знак «плюс». Равенство у(-х) = у(х) также не выполняется, так как знаки перед первыми слагаемыми в этих функциях противоположны. Поэтому данная функция не является ни четной, ни нечетной, т. е. определенной четности не имеет.
Видно, что равенство y(-х) = -y(х) не выполняется, так как перед числом 1 один и тот же знак «плюс». Равенство у(-х) = у(х) также не выполняется, так как знаки перед первыми слагаемыми в этих функциях противоположны. Поэтому данная функция не является ни четной, ни нечетной, т. е. определенной четности не имеет.
г) Область определения данной функции D(у) = (-∞; 2)U(2; ∞) не является симметричной, так как точка х = -2 входит в эту область, а симметричная точка х = -(-2) = 2 не входит. Поэтому данная функция определенной четности не имеет.
Пример 6
Построим график функции ![]()
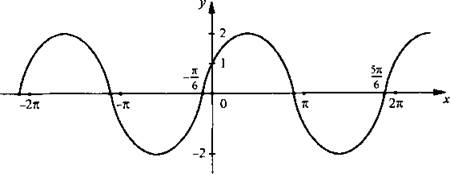
Учтем формулу понижения степени и запишем данную функцию в виде ![]() Теперь построим график y = 2|sinx|. Если sin x ≥ 0, то строим график функции у = 2 sin х. Если sin х < 0, то строим график функции у = -2sin х. Он получается отражением вверх относительно оси абсцисс частей графика у = 2sin х приsin х < 0.
Теперь построим график y = 2|sinx|. Если sin x ≥ 0, то строим график функции у = 2 sin х. Если sin х < 0, то строим график функции у = -2sin х. Он получается отражением вверх относительно оси абсцисс частей графика у = 2sin х приsin х < 0.
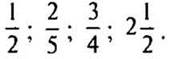
Пример 7
Построим график уравнения cos(x2 + у2) = 1.
Так как выполнено равенство cos(x2 + у2) = 1, то аргумент косинуса х2 + у2 = 2πn, где n – 0, 1, 2, 3, … . При n = 0 получаем уравнение х2 + у2 = 0, которое имеет единственное решение х = у = 0 (начало координат). При n ∈ N получаем уравнение окружности х2 + у2 = 2пn с центром в начале координат и радиуса ![]() Для различных натуральных n получаем семейство концентрических окружностей, радиусы которых
Для различных натуральных n получаем семейство концентрических окружностей, радиусы которых ![]() т. е.
т. е. ![]()
![]() и т. д. Итак, графиком данного уравнения являются начало координат и семейство концентрических окружностей.
и т. д. Итак, графиком данного уравнения являются начало координат и семейство концентрических окружностей.
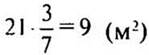
3. Периодичность функций у = sin х, у = cos x
Перейдем к следующему свойству функции – периодичности. Многие реальные явления и процессы имеют повторяющийся (периодический) характер. Например, минутная стрелка занимает одинаковое положение на циферблате часов через каждый час. Такого типа процессы называют периодическими, как и их функции.
Функция f(х) называется периодической с периодом Т (Т – некоторое действительное число, отличное от нуля), если:
1) для любого х из области определения функции значение аргумента х ± Т также принадлежит области определения функции;
2) выполняется равенство f(x + T) = f(x) = f(x – Т). Обычно под периодом функции понимают наименьший из всех положительных периодов (основной период функции).
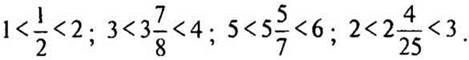
Исходя из определения тригонометрических функций, нетрудно установить, что период функций sin x и cos х составляет 2π, период функций tg х и ctg х – π. Действительно, функции синуса и косинуса определены на всей числовой оси, sin (х + 2π) = sin х и cos (x+ 2π) = cos х для любого х. Аналогично области определения функций тангенса и котангенса включают как точку х, так и точки х ± π. При этом выполняются равенства tg(х + π) = tg х и ctg (х + π) = ctg x.
Пример 8
Докажем, что если функция f(х) периодическая с периодом Т, то при любом целом n ≠ 0 число nТ также период этой функции.
Пусть для определенностиn п = 4. Тогда нужно доказать, что число 4Т является также периодом функции f(х). Найдем ![]()
![]()
![]() Итак, было показано, что для любого х выполнено равенство f(x + 4T) = f(x). Поэтому по определению число 4Т является также периодом функции f(х).
Итак, было показано, что для любого х выполнено равенство f(x + 4T) = f(x). Поэтому по определению число 4Т является также периодом функции f(х).
Пример 9
Найдем период функции ![]()
Предположим, что эта функция периодическая с основным периодом Т. Тогда должно выполняться равенство ![]()
![]() Поэтому получим уравнение
Поэтому получим уравнение ![]() или Т = 2пn, откуда
или Т = 2пn, откуда ![]() Учитывая, что число Т – основной период данной функции, найдем
Учитывая, что число Т – основной период данной функции, найдем ![]()
Аналогично можно показать, что для функции ![]() основной период также
основной период также ![]() для функций
для функций ![]() и
и ![]() основной период
основной период ![]() Это обязательно надо помнить.
Это обязательно надо помнить.
Отметим, что сумма, разность, произведение и частное двух периодических функций могут быть как периодической, так и непериодической функцией. В частности, алгебраическая сумма периодических функций будет функцией периодической, если периоды этих функций соизмеримы (т. е. если их отношение – число рациональное).
Пример 10
Найдем период функции ![]()
Функция f(х) является алгебраической суммой трех периодических функций, периоды которых, соответственно, ![]() Представим эти числа в виде дробей с одинаковыми знаменателями
Представим эти числа в виде дробей с одинаковыми знаменателями ![]()
![]() Видим, что эти числа соизмеримы и их общей мерой является число π/12. Для определения периода f(x) найдем наименьшее общее кратное чисел 12, 8 и 15, которое равно 120. Поэтому
Видим, что эти числа соизмеримы и их общей мерой является число π/12. Для определения периода f(x) найдем наименьшее общее кратное чисел 12, 8 и 15, которое равно 120. Поэтому ![]()
Отметим также, что сложная функция, промежуточным аргументом которой служит периодическая функция, есть функция периодическая. Например, 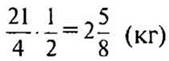 функции периодические.
функции периодические.
Пример 11
Докажем, что функция ![]() непериодическая.
непериодическая.
Функция f(x) является суммой трех периодических функций, периоды которых, равны соответственно 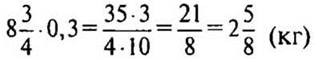 Коэффициенты
Коэффициенты ![]() стоящие перед π, являются несоизмеримыми числами. Числа
стоящие перед π, являются несоизмеримыми числами. Числа ![]() иррациональные и могут быть представлены в виде десятичных бесконечных непериодических дробей. Поэтому нельзя сказать, в какое рациональное число раз такие числа различаются. Следовательно, данная функция непериодическая.
иррациональные и могут быть представлены в виде десятичных бесконечных непериодических дробей. Поэтому нельзя сказать, в какое рациональное число раз такие числа различаются. Следовательно, данная функция непериодическая.
Определение периодической функции может быть использовано для доказательства непериодичности функций.
Пример 12
Докажем, что функция ![]() непериодическая.
непериодическая.
Проведем доказательство от противного. Предположим, что функция периодическая с периодом Т. Тогда должно выполняться равенство ![]() Поэтому имеем уравнение
Поэтому имеем уравнение ![]() Возведем обе части в квадрат:
Возведем обе части в квадрат: ![]() и найдем
и найдем ![]() Видим, что величина Т не является числом и зависит от точки х. Имеется противоречие, и данная функция не является периодической.
Видим, что величина Т не является числом и зависит от точки х. Имеется противоречие, и данная функция не является периодической.
В этом легко убедиться, построив график функции. Ее область определения D(f) = [0; +∞), область значений E(f) = [-1; 1]. Проследим за точками пересечения графика функции с осью абсцисс. Они определяются условием ![]() (где n = 0, 1, 2, …), откуда
(где n = 0, 1, 2, …), откуда 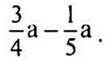 Посчитаем несколько первых таких точек:
Посчитаем несколько первых таких точек: ![]() и т. д. Видим, что расстояние между соседними точками с увеличением jc возрастает. На рисунке приведен график (с нарушением масштаба).
и т. д. Видим, что расстояние между соседними точками с увеличением jc возрастает. На рисунке приведен график (с нарушением масштаба).
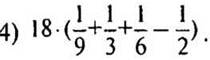
IV. Контрольные вопросы
1. Основные свойства и график функции у = sin х.
2. Свойства функции у = cos x и ее график.
3. Как получить график функции у = cos x, используя график функции у = sin x?
4. Определение периодической функции.
5. Основной период функции.
6. Основной период функций ![]() и
и ![]()
7. Основной период функций ![]() и
и ![]()
V. Задание на уроках
§ 10, № 2 (а, б); 3 (в, г); 5 (а, б); 9 (а); 10 (б); 11 (а, б); 12 (а); 13 (б); 14 (а, б); 15; 16 (a); 17;
§ 11, № 3 (а); 8 (б); 11 (а, б); 12 (в, г); 13 (а);
§ 12, № 1; 3; 7 (а, б); 9 (в, г).
VI. Задание на дом
§ 10, № 2 (в, г); 3 (а, б); 5 (в, г); 9 (б); 10 (а); 11 (в, г); 12 (б); 13 (а); 14 (в, г); 16 (б); 18;
§ 11, № 3 (б); 8 (г); 11 (в, г); 12 (а, б); 13 (б);
§ 13, № 2; 4; 7 (в, г); 9 (а, б).
VII. Творческое задание
Постройте график функции, уравнения или неравенства:
VIII. Подведение итогов уроков














