Цель: использовать производную для исследования функции и построения ее графика.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Дайте полную и упрощенную формулировки признака максимума функции.
2. Определите точки максимума и минимума и промежутки монотонности функции ![]()
3. Найдите стационарные точки функции ![]()
![]()
Вариант 2
1. Дайте полную и упрощенную формулировки признака минимума функции.
2. Определите точки максимума и минимума и промежутки монотонности функции ![]()
3. Найдите стационарные точки функции ![]()
![]()
III. Изучение нового материала
При исследовании функции и построении ее графика надо:
1. Найти область определения.
2. Выяснить особенности (четность или нечетность функции, периодичность и т. д.).
3. Найти точки пересечения графика с осями координат.
4. Найти промежутки знакопостоянства.
5. Выяснить с помощью производной монотонность функции, промежутки возрастания и убывания.
6. Используя производную, найти точки экстремума и значения функции в этих точках.
7. Определить вертикальные, горизонтальные или наклонные асимптоты, исследовав поведение функции в окрестности особых точек и при больших по модулю x.
Рассмотрим применение этого плана для исследования функции и построения ее графика.
Пример 1
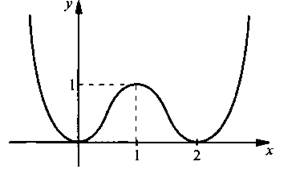
Исследуем функцию f(x) = х2(х – 2)2 и построим ее график.
1. Область определения D(f) = R, так как f(х) – многочлен.
2. Функция определенной четности не имеет.
3. График касается оси абсцисс в точках x = 0 и х = 2.
4. При всех значениях х функция f(х) ≥ 0.
5. 6. Найдем производную функции: ![]()
![]() Производная существует при всех значениях х и обращается в нуль при х1 = 0, х2 = 1 и х3 = 2 (стационарные точки). Отметим эти точки на числовой оси и нарисуем диаграмму знаков производной.
Производная существует при всех значениях х и обращается в нуль при х1 = 0, х2 = 1 и х3 = 2 (стационарные точки). Отметим эти точки на числовой оси и нарисуем диаграмму знаков производной.
Видно, что промежутки убывания функции (-∞; 0] и [1; 2] и промежутки возрастания [0; 1] и [2; ∞). В точках х = 0 и х = 2 функция имеет минимум и fmjn = f(0) = f(2) = 0. В точке x = 1 функция имеет максимум и fmах = f(1) = 1.
7. Асимптот график функции не имеет. Учитывая проведенное исследование функции, нарисуем ее график.
Пример 2
Проведем исследование и построим график функции ![]()
1. Область определения функции ![]()
2. Так как область определения – несимметричное множество, то функция определенной четности не имеет.
3. График пересекает ось ординат в точке f(0) = 1. Для нахождения точек пересечения с осью абсцисс решим уравнение f(х) = 0 или 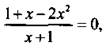 корни которого x1 = -1/2 и x2= 1.
корни которого x1 = -1/2 и x2= 1.
4. Отметим точки x1 = -1/2, x2 = 1 и х = -1 (в которой дробь не имеет смысла) на координатной оси и отметим знаки функции f(х). Видно, что значения f(х) > 0 при ![]() и значения f(х) < 0 при
и значения f(х) < 0 при ![]() – промежутки знакопостоянства функции.
– промежутки знакопостоянства функции.
5. 6. Найдем производную функции: ![]()
![]() Производная не существует в точке х = -1, но эта точка не входит в область определения функции и не является критической.
Производная не существует в точке х = -1, но эта точка не входит в область определения функции и не является критической.
Производная обращается в нуль в точках х = -2 и х = 0 (стационарные точки). Отметим эти точки на числовой оси и расставим знаки производной. Видно, что функция f(х) убывает на промежутках (-∞; -2] и [0; ∞) и возрастает на промежутках [-2; -1) и (-1; 0]. В точке х = -2 функция имеет минимум и fmin = f(-2) = 9, в точке х = 0 имеет максимум иfmах = f(0) = 1.
7. Функция имеет вертикальную асимптоту х = -1, так как при х → -1 числитель дроби 1 + х – 2х2 → -2, а знаменатель х + 1 → 0. Поэтому f(х) → ±∞ при х → -1.
В функции f(х) выделим целую часть (деля уголком) и получим: ![]() При х→ ±∞ величина
При х→ ±∞ величина ![]() и f(х) → -2х + 3. Поэтому функция f(х) имеет наклонную асимптоту у = -2х + 3. Учитывая проведенное исследование, строим график данной функции.
и f(х) → -2х + 3. Поэтому функция f(х) имеет наклонную асимптоту у = -2х + 3. Учитывая проведенное исследование, строим график данной функции.
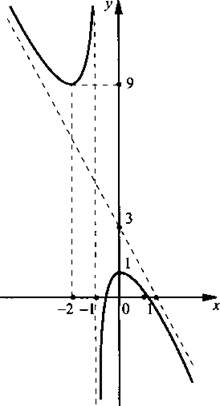
Пример 3
Определим число корней уравнения х4 – 4х3 + 8 = 0.
Рассмотрим и исследуем функцию f(x) = х4 – 4х3 + 8. Найдем производную этой функции: f'(x) = 4х3 – 12×2 = 4х2(x – 3). Приравняем производную нулю и найдем стационарные точки функции х = 0 и х = 3. Нарисуем диаграмму знаков производной.
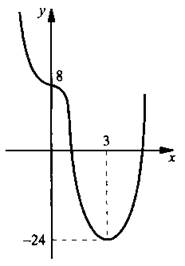
Видно, что на промежутке [3; ∞) функция возрастает. В точке х = 3 функция имеет минимум fmin(x) = f(3) = -19. Тогда по теореме о корне уравнение имеет один корень на промежутке (∞; 3) и один корень на промежутке (3; ∞). Таким образом, данное уравнение имеет два корня (на рисунке приведен график).
Пример 4
Найдем все значения параметра а, при которых уравнение ![]() имеет решения.
имеет решения.
Используем формулу понижения степени, запишем уравнение в виде ![]() и выразим
и выразим ![]() Введем новую переменную t (где
Введем новую переменную t (где ![]() ) и построим график функции a(t). Приравняем производную a’ = 6t2 – 8 нулю и получим стационарные точки
) и построим график функции a(t). Приравняем производную a’ = 6t2 – 8 нулю и получим стационарные точки 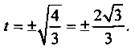 Отметим эти точки на числовой оси и расставим знаки производной. Стационарные точки функции не принадлежат промежуткам [-1; 0)U(0; 1]. Поэтому на этих промежутках функция убывает. Учтем, что функция a(t) нечетная. Найдем значения а(-1) = 6 и a(1) = -6. На рассматриваемых промежутках построим график функции.
Отметим эти точки на числовой оси и расставим знаки производной. Стационарные точки функции не принадлежат промежуткам [-1; 0)U(0; 1]. Поэтому на этих промежутках функция убывает. Учтем, что функция a(t) нечетная. Найдем значения а(-1) = 6 и a(1) = -6. На рассматриваемых промежутках построим график функции.
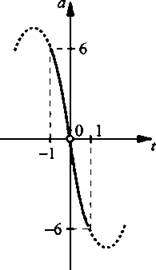
На графике видно, что при ![]() данное уравнение имеет решения.
данное уравнение имеет решения.
IV. Задание на уроке
§ 31, № 1 (а); 2 (б); 5 (а, б); 6 (в, г); 7 (а); 8 (в, г); 9 (а); 10 (б); 11 (а); 12 (б); 13; 15.
V. Задание на дом
§ 31, № 1 (б); 2 (а); 5 (в, г); 6 (а, б); 7 (в); 8 (а, б); 9 (в); 10 (а); 11 (б); 12 (a); 14.
VI. Подведение итогов урока














