Цель: рассмотреть формулы приведения и их применение.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант I
1. Используя числовую окружность, дайте определение cos t.
2. Решите неравенство 
3. Постройте график уравнения tg(y + х) = 1.
Вариант 2
1. Используя числовую окружность, дайте определение sin t.
2. Решите неравенство 
3. Постройте график уравнения ctg(y -х) = 1.
III. Изучение нового материала
Выражения 
и т. д. можно записать проще: sit t, sin t, ctgt соответственно. Для этого используют формулы приведения. По сути, это не формулы, а определенный алгоритм преобразований.
При преобразовании тригонометрической функции 
где п ∈ Z, надо знать следующее.
1) Если n – четное число, то преобразуемая функция не меняется. Если n – нечетное число, то преобразуемая функция меняется на кофункцию (<сопряженную функцию). Аргументом преобразованной функции будет t. Заметим, что кофункциями являются пары функций: синус и косинус; тангенс и котангенс.
2) Знак преобразованной функции совпадает со знаком исходной функции при условии, что угол t острый, т. е. t ∈ (0; π/2) (хотя реально он может быть любым). Знаки тригонометрических функций по координатным четвертям представлены на рисунке.
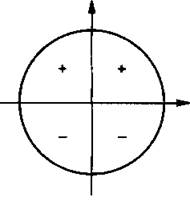
Знаки синуса
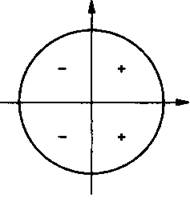
Знаки косинуса
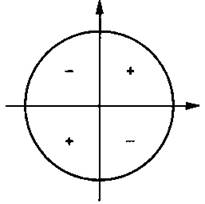
Знаки тангенса и котангенса
Пример 1
Упростим выражение 
Так как функция котангенса имеет аргумент 
и число n = 3 нечетное, то функция котангенса меняется на кофункцию – тангенс. В предположении, что угол а острый, получим, что угол 
лежит в IV четверти. В этой четверти знак котангенса отрицательный. В I четверти (угол а острый) все тригонометрические функции положительны (в том числе и тангенс). Поэтому перед тангенсом необходимо поставить знак «минус». В итоге имеем: 
Пользуясь этим алгоритмом (формулами приведения), рассмотрим еще ряд задач.
Пример 2
Упростим следующие выражения:
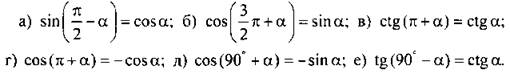
Пример 3
Приведем к тригонометрической функции угла из промежутка 
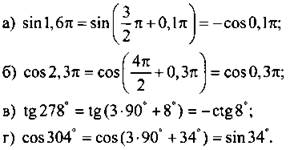
Пример 4
Упростим выражение:
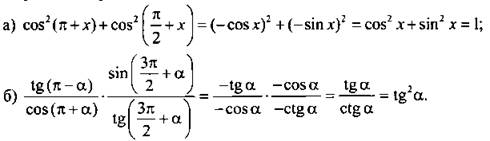
IV. Контрольный вопрос (фронтальный опрос)
На примерах поясните формулы приведения.
V. Задание на уроке
§ 9, № 1; 3; 5 (а, б); 6 (в, г); 7 (а, б); 8 (а); 9 (в, г); 10 (а); 11 (б); 12 (а, в); 13 (а); 14(6).
VI. Задание на дом
§ 9, № 2; 4; 5 (в, г); 6 (а, б); 7 (в, г); 8 (б); 9 (а, б); 10 (б); 11 (а); 12 (б, г); 13 (б); 14 (а).
VII. Подведение итогов урока
