Цели: ввести правило сложения отрицательных чисел на конкретной задаче; добиться усвоения учащимися правила сложения отрицательных чисел и умения применять его при выполнении сложения; прививать каждому ученику вкус к самостоятельной, активной творческой деятельности; развивать познавательный интерес к предмету.
Ход урока
I. Организационный момент
«Презирай лень мысли!» (В. А. Сухомлинский)
— Это девиз нашего урока. Как вы понимаете эти слова? Что они значат для вас?
II. Устный счет
1. Найдите значение выражения:
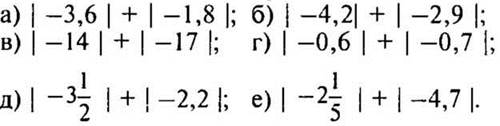
2. Сравните числа: а) —9,8 и 0,7; б) —5,028 и —5,28; в) —5/12 и —7/12.
3. Из полной бочки отлили сначала 60% всей воды, затем еще 60 л. После этого бочка оказалась пустой. Сколько литров воды было в бочке?
4. Для покупки порции мороженого у Пети не хватало семи рублей, а у Маши — одного рубля. Тогда они сложили имевшиеся у них деньги. Но их также не хватило на покупку одной порции мороженого. Сколько стоила порция мороженого?
Решение:
Если бы у Пети был хотя бы рубль, то он дал бы Маше, и им хватило бы на мороженое (ведь ей не хватало всего рубля). Следовательно, у Пети денег не было совсем, а так как ему не хватало на мороженое 7 рублей, то мороженое стоило 7 рублей.
III. Сообщение темы урока
— Еще во II веке до нашей эры китайский император Ши Хуан Ди, разгневавшись на ученых, повелел все научные книги сжечь, а их авторов и читателей казнить. Содержание этих книг дошло до нас лишь в отрывках, откуда известно, что китайцы не знали правила сложения отрицательных чисел. Впервые их сформулировали индийские ученые.
Вот видите, китайцы не смогли вывести правило сложения отрицательных чисел в свое время, а мы сегодня на уроке постараемся дойти до истины.
IV. Изучение нового материала
1. Практическая работа.
— Найдите сумму чисел с помощью координатной прямой (на доске заранее нарисованы координатные прямые).
(Учащиеся по одному выходят к доске и выполняют сложение на координатной прямой.)
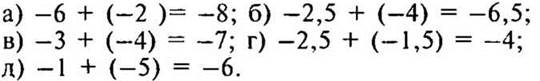
2. Работа над новой темой.
— Сравните данные выражения. Что общего? (Везде надо найти сумму двух отрицательных чисел, результат сложения — отрицательное число.)
— Чем отличается? (Разные слагаемые.)
— Рассмотрим первое выражение: —6 + (—2 ) = —8.
— Как получить число 8, не учитывая знаков? (Сложить числа 6 и 2.) Что сложили? (Модули чисел —6 и —2.)
— Проверьте, так ли это для других выражений.
— Сформулируйте правило сложения отрицательных чисел.
— Прочитайте это правило в учебнике на стр. 176. Сравните правило, которое сформулировали вы и с правилом в учебнике.
Правило:
Чтобы сложить два отрицательных числа, нужно:
1) сложить модули слагаемых;
2) перед полученным числом поставить знак «—».
V. Закрепление изученного материала
1. № 1045 стр. 177.
(Первый столбик — цепочкой, учащиеся устно проговаривают решение, третий столбик под контролем учителя — один ученик у доски решает, проговаривая правило сложения отрицательных чисел. Второй столбик учащиеся выполняют самостоятельно, после производится проверка ответов.)
(Ответы:
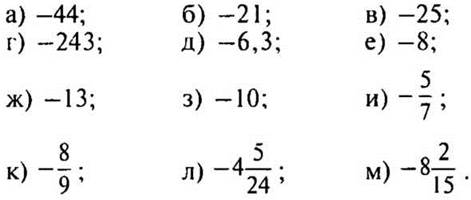 )
)
2. № 1046 стр. 177 (устно).
— Нужно ли находить значение выражения —17 + (—31)? (Нет.)
— Почему? (Мы знаем, что любое число от прибавления положительного числа увеличивается, а от прибавления отрицательного числа уменьшается, следовательно, данное выражение
— 17 + (—31) меньше —17, так как к числу —17 прибавили отрицательное число, следовательно, сумма меньше 1 слагаемого.)
VI. Физкультминутка
VII. Работа над задачей
№ 991 стр. 166 (с подробным комментированием на доске и в тетрадях).
— Сколько четырехугольных пирамид составляют куб? (6.)
— Зная, что ребро куба равно 1,2 см, что можно найти? (Объем куба.)
— Чему равен объем куба? Запишите формулу.
— Зная объем куба и что куб состоит из 6 равных четырехугольных пирамид, что можно найти? (Объем одной четырехугольной пирамиды.)
— Что для этого надо сделать? (Разделить объем куба на 6.)
— Во второй части задачи известно, что объем одной пирамиды равен 1/6 см3. Зная это, что можно узнать? (Объем нового куба.)
— Зная объем нового куба, можно узнать ребро куба? (Да.)
— Как найти ребро куба? (Методом подбора.)
Решение:
V = а3
1) 1,23 = 1,728 см3 — объем куба с ребром 1,2 см.
2) 1,728 : 6 = 0,288 см3 — объем одной пирамиды.
3) 1/6 · 6 = 1 см3 — объем нового куба.
4) Так как объем куба равен а3 = 1, то ребро нового куба равно 1 см.
(Ответ: 0,288 см3; 1 см.)
VIII. Повторение изученного материала
№ 1060 (в) стр. 179 (на обратной стороне доски, самопроверка).
— Как выполняется деление дробей? (Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.)
Решение:
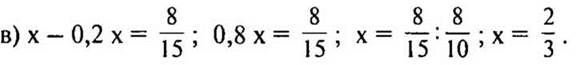
(Ответ: х = 2/3.)
IX. Самостоятельная работа (5—7 мин)
Вариант I
Найдите значение суммы:
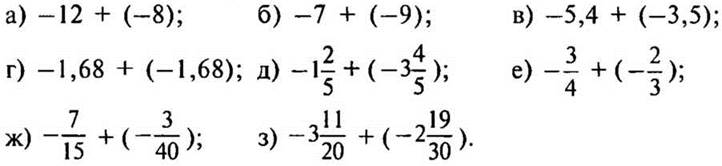
Вариант II
Найдите значение суммы:
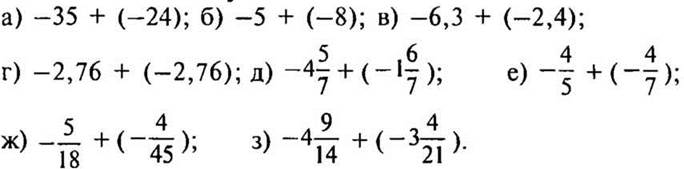
X. Подведение итогов урока Домашнее задание
№ 1056 (а-е) стр. 178, № 1057 (а), 1058, 1060 (а) стр. 179.














