Цели: формировать навык сравнения рациональных чисел; проверить знания, умения по изученной теме; развивать умение самостоятельно работать; воспитывать уверенность в себе, в своих знаниях.
Ход урока
I. Организационный момент
II. Устный счет
1. Сравните числа:
а) -7,23 и -2; б) -7,08 и -7,008; в) 54,34 и 0; г) 0 и -234; д) -5 и -14; е) 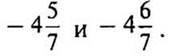
2. В каком случае верно равенство:
а) | а | = а; б) | а | = —а; в) | —а | = —а; в) | —а | = а.
3. В школе 11/24 всех учащихся — ученики начальных классов. Сколько учеников в школе, если в старших классах 260 человек?
4. Лифт поднимается с 1 этажа на 3-й за 6 сек. За сколько секунд он поднимется с 1 этажа на 5-й? (1 пролет — 2 сек, 4 пролета (с 1 этажа на 5-й) — 8 сек.)
5. По стеблю растения, высота которого 1 м, от земли ползет гусеница. Днем она поднимается на 3 дм, а ночью опускается на 2 дм. Через сколько суток гусеница доползет до верхушки растения? (Через 7 суток.)
6. Как появились знаки + и —? Кто их ввел как математические знаки и в каком веке? (Знаки «+» и «—» широко использовали в торговле. Виноделы на пустых бойках ставили «—», означавший убыль. Если бочку наполняли, то знак перечеркивали и получали «+», означавший прибыль. Эти знаки как математические ввел Ян Видман в XV веке.)
III. Сообщение темы урока
— Сегодня на уроке мы продолжим сравнивать числа.
IV. Закрепление изученного материала
1. Вместо предложения «Число a — число положительное» можно записать: а > 0; вместо предложения «Число a — число отрицательное» можно записать: а < 0; вместо предложения «Число a — число неотрицательное» можно записать: а ≥ 0.
2. № 977 стр. 164 (устно).
— Что значит назвать числа в порядке возрастания? (Первым назвать наименьшее число, последним наибольшее число.)
— Что значит назвать числа в порядке убывания? (Называть числа от большего числа к меньшему.)
3. № 980 стр. 165 (с подробным комментированием у доски и в тетрадях, учащиеся к доске выходят цепочкой по одному).
Решение:
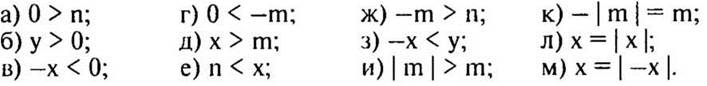
V. Работа над задачей
№ 993 (2) стр. 166 (на обратной стороне доски, самопроверка).
Решение:
1) 0,16 + 0,52 + 0,12 = 0,8 (кг) — чайная смесь.
2) 0,16 : 0,8 = 1,6 : 8 = 0,2 = 20% – грузинского чая содержится в чайной смеси.
3) 0,52 : 0,8 = 0,65 = 65% — азербайджанского чая содержится в чайной смеси.
4) 0,12 : 0,8 = 0,15 = 15% – индийского чая содержится в чайной смеси.
(Ответ: 20%, 65%, 15%.)
VI. Физкультминутка
VII. Повторение изученного материала
Решите уравнения:
1) | —х — 1 | = 9;
2) | 2х + 13| = 0;
3) | 3х – 4 | = 10.
VIII. Самостоятельная работа (10 мин)
Вариант I
1. Сравните числа:

2. Найдите модуль числа: 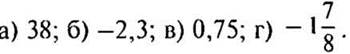
3. Точка К (—3) при перемещении на 5 перешла в точку М. Найдите координату точки М.
4. Запишите все целые числа, которые являются одновременно решениями неравенств: -4 < х < 6 и -7 < х < 3.
Вариант II
1. Сравните числа:
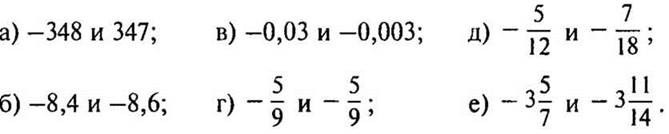
2. Найдите модуль числа: 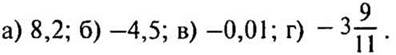
3. Найдите координату точки А, если при перемещении на —9 она перешла в точку В (—2).
4. Запишите все целые числа, которые являются одновременно решениями неравенств: —5 < х < 4 и —2 < х < 7.
IX. Подведение итогов урока
— Как можно с помощью знаков неравенства записать:
а) число b — число положительное;
б) число а — число отрицательное;
в) число а — число неотрицательное?
— Положительным или отрицательным будет число с, если:
а) с < 0; б) с > 0; в) с = 0.
Домашнее задание
№ 997, 999, 1000 стр. 167.














