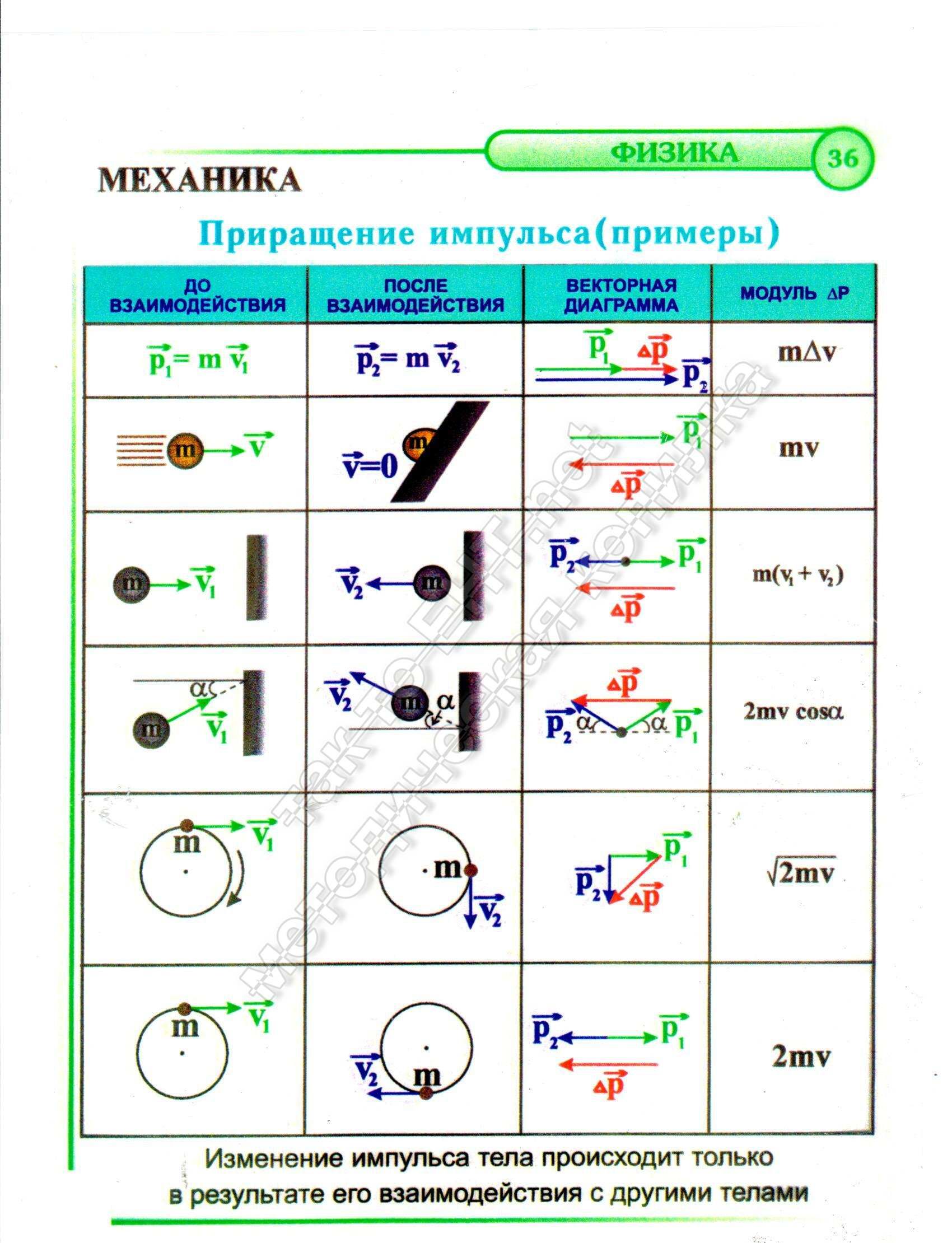
Цели урока:
· Образовательные – повторение, обобщение и проверка знаний по теме: “Метод геометрических мест”; выработка основных навыков.
· Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
· Воспитательные – посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.
Задачи урока:
· Формировать навыки в построении геометрических фигур с помощью циркуля, масштабной линейки, транспортира и чертежного треугольника.
· Проверить умение учащихся решать задачи.
План урока:
1. Введение.
2. Теоретическая часть.
3. Определение геометрического места точек.
4. Сущность метода геометрических мест.
5. Основные геометрические места точек на плоскости.
6. Примеры задач на геометрические места точек.
Введение.
Геометрия – это наука о свойствах геометрических фигур. Слово «геометрия» греческое, в переводе на русский язык означает «землемерие». Такое название этой науке было дано потому, что в древнее время главной целью геометрии было измерение расстояний и площадей на земной поверхности.
Легко представить себе поверхность как границу тела: плоская поверхность стола, сферическая поверхность мяча, цилиндрическая поверхность трубы. Но такое представление не полно. Возьмем тонкую замкнутую проволоку изогнутой формы и опустим её в мыльную пену. Если мы осторожно извлечем её из пены, то увидим, что просвет в проволочном “кольце” затянут тончайшей мыльной пленкой. Правильно представлять себе поверхность именно как тонкую пленку (но лишенную всякой толщины).
Легко представить себе поверхность как границу тела: плоская поверхность стола, сферическая поверхность мяча, цилиндрическая поверхность трубы. Но такое представление не полно. Возьмем тонкую замкнутую проволоку изогнутой формы и опустим её в мыльную пену. Если мы осторожно извлечем её из пены, то увидим, что просвет в проволочном “кольце” затянут тончайшей мыльной пленкой. Правильно представлять себе поверхность именно как тонкую пленку (но лишенную всякой толщины).
Важнейшая и простейшая поверхность – плоскость. Прямая m, лежащая в плоскости, разбивает её на две части – полуплоскости; точки этой прямой и только они являются общими точками обеих полуплоскостей. Если А – точка одной полуплоскости, а В – другой, то отрезок АВ пересекает границу m полуплоскостей в некоторой точке С, лежащей между А и В.
Плоскости задаются тремя точками и обозначаются часто так: плоскость АВС или PQR и т.д. Иногда бывает проще обозначать плоскость одной буквой греческого алфавита: a, b, g, d…
Под фигурой обычно понимают некоторое сочетание определенным образом расположенных в одной плоскости (а иногда и в пространстве) элементов: точек, прямых, лучей, отрезков (иногда и плоскостей).
Под телом понимают обычно часть пространства, ограниченную какой-либо замкнутой поверхностью. Так, конус – тело, ограниченное канонической поверхностью с боков и плоским круглым основанием снизу. Куб – тело, ограниченное шестью квадратными гранями, и т.д. Курс геометрии традиционно подразделяется на планиметрию и стереометрию; в планиметрии рассматриваются свойства различных фигур (треугольников, многоугольников, окружностей), лежащих в плоскости. В стереометрии изучаются свойства пространственных фигур и тел.
Один из основных способов задания фигур на плоскости заключается в указании свойства, которому удовлетворяют точки этой фигуры.
Вспомним определение окружности. Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, удаленных от данной точки на данное расстояние. Свойством здесь является удаленность от данной точки на данное расстояние.
Фигуры, состоящие из всех точек, удовлетворяющих заданному свойству, получили особое название «геометрические места точек». Таким образом, геометрическим местом точек называется фигура, состоящая из всех точек, удовлетворяющих заданному свойству или нескольким заданным свойствам.
Поясним смысл слов “всех точек, удовлетворяющих заданному свойству” в этом определении. Они означают, что все точки, принадлежащие фигуре, удовлетворяют заданному свойству, и наоборот, все точки, удовлетворяющие заданному свойству, принадлежат фигуре. Другими словами, точка принадлежит фигуре в том и только том случае, когда для нее выполняется заданное свойство.
Рассмотрим еще несколько геометрических мест точек.
Серединным перпендикуляром к заданному отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.
Выясним, каким геометрическим местом точек является серединный перпендикуляр.
Теоретическая часть.
Файл:T.gif Теорема. Серединный перпендикуляр к отрезку является геометрическим местом точек, одинаково удаленных от концов этого отрезка.
Доказательство. Пусть дан отрезок АВ и точка О – его середина. Покажем, что геометрическим местом точек, одинаково удаленных от точек А и В является серединный перпендикуляр к отрезку АВ (рис. 1). Действительно, очевидно, точка О одинаково удалена от точек А, В и принадлежит серединному перпендикуляру. Если точка С одинаково удалена от точек А и В и не совпадает с точкой О, то треугольник АВС равнобедренный и СО – медиана. По свойству равнобедренного треугольника медиана является также и высотой. Значит, точка С принадлежит серединному перпендикуляру. Обратно, пусть точка С принадлежит серединному перпендикуляру и не совпадает с О, тогда прямоугольные треугольники АОС и ВОС равны (по катетам). Следовательно, АС=ВС.
Файл:09022011 0.gif
Файл:T.gif Теорема. Биссектриса угла является геометрическим местом точек, лежащих внутри данного угла и одинаково удаленных от его сторон.
Доказательство. Рассмотрим угол c вершиной в точке О и сторонами а, b. Пусть точка С лежит внутри данного угла. Опустим из нее перпендикуляры СА и CB на стороны а и b (рис. 2). Если CA = CB, то прямоугольные треугольники АOС и ВOС равны (по гипотенузе и катету). Следовательно, углы AOC и BOC равны. Значит, точка C принадлежит биссектрисе угла. Обратно, если точка C принадлежит биссектрисе угла, то прямоугольные треугольники AOC и BOC равны (по гипотенузе и острому углу). Следовательно, AC = BC. Значит, точка С одинаково удалена от сторон данного угла.
Определение геометрического места точек.
Геометрическое место точек
Пример 1. Срединный перпендикуляр любого отрезка есть геометрическое место точек (т.е. множество всех точек), равноудалённых от концов этого отрезка. Пусть PO AB и AO = OB:
Тогда, расстояния от любой точки P, лежащей на срединном перпендикуляре PO, до концов A и B отрезка AB одинаковы и равны d. Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.
Пример 2. Окружность – это геометрическое место точек (т.е. множество всех точек), равноудалённых от её центра (одна из этих точек – А).
Окружность
Тогда отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается r или R. Часть плоскости, ограниченная окружностью, называется кругом. Часть окружности AmB, называется дугой. Прямая PQ, проходящая через точки M и N окружности, называется секущей, а её отрезок MN, лежащий внутри окружности – хордой. Хорда, проходящая через центр круга например, BC называется диаметром и обозначается d или D.
Диаметр – это наибольшая хорда, равная двум радиусам (d = 2r). Предположим, дана точка А (7; 3; 5); эта запись означает, что точка А определяется координатами х = 7, у = 3, z = 5. Если масштаб для построения чертежа задан или выбран, то откладывают на оси х от некоторой точки О отрезок ОАХ, равный 7 единицам, и на перпендикуляре к этой оси, проведенном из точки Ах, отрезки АХА’ = 3 ед. и АХА” = 5 ед. Получаем проекции А’ и А”. Для построения достаточно взять только ось х. Принимая оси проекций за оси координат, можно найти координаты точки по данным ее проекциям. Например, отрезок ОАХ – выражает абсциссу точки А, отрезок АХА’ – ее ординату, отрезок АХА” – аппликату. Если задается лишь абсцисса, то этому соответствует плоскость, параллельная плоскости, определяемой осями у и z.
Действительно, такая плоскость является геометрическим местом точек, у которых абсциссы равны заданной величине. Если задаются две координаты, то этим определяется прямая, параллельная соответствующей координатной оси.
Сущность метода геометрических мест.
Сущность метода геометрических мест, используемого при решении задач, состоит в следующем. Пусть, решая задачу, нам надо найти точку X, удовлетворяющую двум условиям. Геометрическое место точек, удовлетворяющих первому условию, есть некоторая фигура F1, а геометрическое место точек, удовлетворяющих второму условию, есть некоторая фигура F2. Искомая точка X принадлежит F1 и F2 т. е. является их точкой пересечения. Если эти геометрические места простые (скажем, состоят из прямых и окружностей), то мы можем их построить и найти интересующую нас точку X.
Ломаной А1А2А3…An называется фигура, которая состоит из точек А1, А2, …, An и соединяющих их отрезков А1A2, A2A3, …, An-1, An. Точки А1, А2, …, Аn называются вершинами ломаной, а отрезки A1A2, A2A3, …, An-1, An – звеньями ломаной. Ломаная называется простой, если она не имеет самопересечений.
А1A2A3A4 – простая ломаная из трёх звеньев.
Ломаная называется замкнутой, если у неё концы совпадают. Простая замкнутая ломаная называется многоугольником, если её соседние звенья не лежат на одной прямой. Вершины ломаной называются вершинами многоугольника, а звенья ломаной – сторонами многоугольника. Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями. Многоугольник с n-вершинами, а значит, и с n-сторонами называется n-угольником.
Плоским многоугольником и многоугольной областью называется конечная часть плоскости, ограниченная многоугольником.
Плоским многоугольником и многоугольной областью называется конечная часть плоскости, ограниченная многоугольником.
Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.
Многоугольник называется невыпуклым, если он оказывается лежащим по обе стороны прямой, содержащей любую его сторону.
Основные геометрические места точек на плоскости.
Геометрическим местом точек плоскости, равноудалённых от сторон угла, будет биссектриса данного угла. АК = AT, где А – любая точка на биссектрисе.
Геометрическим местом точек плоскости, равноудалённых от заданной точки, будет окружность с центром в этой точке. Точка О равноудалена от точек окружности.
Местоположение центра окружности, вписанной в треугольник.Центр окружности, вписанной в треугольник,является точкой пересечения его биссектрис. В ⊿ABC отрезки AT и СК являются биссектрисами.
Геометрическим местом точек, находящихся на данном расстоянии h от данной прямой а , есть пара прямых m1 и m2, параллельных а и находящихся от нее на расстоянии h.
Файл:09022011 9.gif
Геометрическим местом точек, равноудаленных от двух данных параллельных прямых m1 и m2, есть прямая а , параллельная m1 и m2, проходящая через С середину отрезка секущей С.
Файл:09022011 10.gif
Геометрическим местом точек, равноудаленных от двух данных пересекающихся прямых d1 и d2, представляет собой две взаимно перпендикулярные прямые m1 и m2, являюшиеся биссектрисами углов, образованных данными прямыми.
Файл:09022011 11.gif
Примеры задач на геометрические места точек.
Задача №1.
Найдите геометрическое место центров окружностей, проходящих через две данные точки.
Решение: Пусть окружность с центром O проходит через данные точки A и B. Поскольку OA = OB (как радиусы одной окружности), точка O лежит на серединном перпендикуляре к отрезку AB. Обратно, каждая точка O, лежащая на серединном перпендикуляре к AB, равноудалена от точек A и B. Значит, точка O — центр окружности, проходящей через точки A и B.
Задача №2.
Дан прямоугольник ABCD. Найдите ГМТ X, для которых AX + BX = CX + DX.
Решение: Пусть l — прямая, проходящая через середины сторон BC и AD. Предположим, что точка X не лежит на прямой l, например что точки A и X лежат по одну сторону от прямой l. Тогда AX < DX и BX < CX, а значит, AX + BX < CX + DX. Поэтому прямая l — искомое ГМТ.
Задача №3. На данной прямой найдите точку одинаково удаленную от двух заданных точек.
Решение: Пусть c – данная прямая, A, B – данные точки (рис. 3). Геометрическим местом точек, одинаково удаленных от точек A и B, является серединный перпендикуляр к отрезку AB. Если серединный перпендикуляр и прямая c пересекаются, то искомой точкой C будет их точка пересечения. Если они не пересекаются, то задача не имеет решения.
Задача №4.
Найдите точки, одинаково удаленные от прямых, на которых лежат стороны данного треугольника.
Решение: Рассмотрим треугольник ABC (рис. 4). Точка D этого треугольника одинаково удалена от AB и AC, если она принадлежит биссектрисе угла A. Аналогично, точка D треугольника ABC одинаково удалена от AB и BC, если она принадлежит биссектрисе угла B. Таким образом, точкой одинаково удаленной от AB, AC и BC будет точка пересечения биссектрис углов A и B треугольника ABC.
Задача №5.
Построить треугольник по a, b и углу В=b при основании.
Решение: Предположим, что задача решена и треугольник АВС (рис. 11) – искомый. Построить этот треугольник можно, если знать, например, положение всех его вершин. Положение вершин В и С можно считать известным, тогда остается найти точку А. А – искомая точка. Чтобы найти искомое, надо знать его геометрические вытекающие из условия задачи свойства. Первое свойство точки А: она является вершиной треугольника с основанием ВС=а и данным углом АВС при основании. Следовательно, точка А принадлежит ГМТ 4, т. е. лучу ВА (составляющему с основанием ВС угол b) или лучу ВАў, являющемуся образом ВА при симметрии относительно ВС. Однако положение точки А на плоскости (относительно точек В и С) по одному этому свойству найти не удастся. Выясним второе свойство точки А. Оно очевидно: точка А удалена от точки С на данное расстояние b, т. е. А принадлежит ГМТ 1 – окружности (С,b).
Файл:09022011 14.gif
Интересный факт:
“Как вы думаете, что общего между египетскими пирамидами, картиной Л. да Винчи “Мона Лиза”, строением тела человека, подсолнухом, улиткой, строением галактик, микробов и вирусов, молекулы ДНК, законами физики, снежинками или растениями?
Ответ на этот вопрос сокрыт в удивительных числах и пропорции, которые были обнаружены математиком средневековья Леонардо Фибоначчи.
Оказывается, все мироздание, все живое на планете и даже человек наделены физическими пропорциями Божественного сечения. Эта вездесущность Золотого числа указывает нам ясную связь всего живого сущего на планете. Всевышний Господь сотворил и избрал эту Золотую меру как строительные шифр для создания нашего прекрасного мира. Ученые и люди искусства лишь изучают этот закон и стараются подражать ему.”
Вопросы:
1. Сформулируйте определение окружности?
2. Что такое фигура?
3. Какая разница между диаметром и радиусом?
4. Какая пропорция метода золотого сечения?