Цели: отрабатывать умение находить дроби от числа, решать задачи на нахождение дроби от числа с помощью умножения; развивать умение анализировать, сравнивать, делать выводы, логическое мышление.
Ход урока
I. Организационный момент
«Счет и вычисления — основа порядка в голове» (И. Песталоцци).
II. Устный счет
1. Вычислите: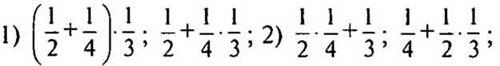 
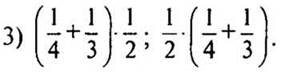
2. Найдите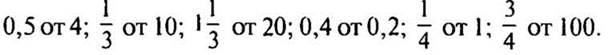 
3. Брат старше сестры во столько раз, сколько ему лет. Сколько лет сестре? (1 год.)
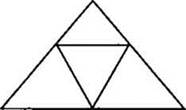
4. Разделите треугольник на 4 равных треугольника.
Ответ:
5. Найти сумму: 6 + 12 + 18 + … + 90 + 96.
Решение:
1) 6n = 96, n = 16;
2) 6 + 96 = 102;
3) 102 · (16 : 2) = 816.
(Ответ: 816.)
III. Сообщение темы урока
Продолжим решать задачи на нахождение дроби от числа с помощью умножения.
IV. Изучение нового материала
№ 487—489 стр. 80 (у доски и в тетрадях).
— Прочитайте задачи.
— Сравните текст задач.
— Что общего? (В книге 140 страниц)
— Чем отличается?
— Сравните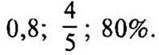 
(Это разная форма записи одного и того же числа.)
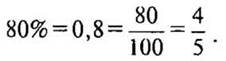
— К какому типу задач относятся эти задачи?
— Как найти дробь от числа?
— Запишите решение:
1) 140 · 0,8 = 112 (стр.).
2) 
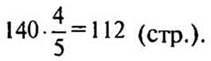(стр.).
3) 80% = 0,8.
140 · 0,8 = 112 (стр.).
(Ответ: 112 страниц прочитал каждый мальчик.)
— Какой вывод можно сделать?
V. Закрепление изученного материала
№ 485 стр. 80 (устно)
— Сколько равных частей составляют квадрат ABCD? (16.)
— Сколько равных частей составляют квадрат AEFP? (4.)
— Как узнать, какую часть меньший квадрат составляет от большего?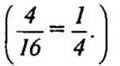 
(Ответ: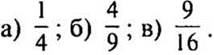 
)
VI. Физкультминутка
VII. Работа над задачей
1. № 493 стр. 81 (самостоятельно, самопроверка, образец на доске).
Решение:
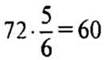(рис.) — выполнены акварелью.
72 — 60 = 12 (рис.) — остальные.
12 · 0,25 = 12 : 4 = 3 (рис.) — выполнены карандашом.
(Ответ: 3 рисунка.)
2. № 500 стр. 81 (у доски и в тетрадях).
Решение:
Пусть 1 — вся книга.
1) 
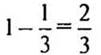(части) — книги осталось прочитать после первого дня.
2) 
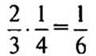(часть) — книги прочитала Ира во второй день.
3) 
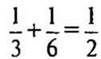(часть) – книги прочитана за два дня.
(Ответ: 1/2 часть.)
3. В течение первой половины года цена на товар выросла на 20%, а в течение второй половины года — на 15%. На сколько процентов поднялась цена за этот год?
— Как вы считаете, можно ли ответить на вопрос задачи, сложив 20% и 15%? Почему?
— На сколько процентов выросла цена товара за первую половину года?
— Во сколько раз она увеличилась по отношению к первоначальной цене?
— Как изменилась цена за вторую половину года?
— Во сколько раз она увеличилась по отношению к цене за первую половину года?
— Что требуется узнать в задаче?
Решение:
Пусть х руб. — первоначальная цена товара.
1) 100 + 20 = 120% – от первоначальной цены.
120% = 1,2
1,2х руб. — цена в конце первой половины года.
2) 1,2х рублей — 100%
100 + 15 = 115%
115% от 1,2х (руб.) — цена в конце года.
115% = 1,15
1,15 · 1,2х = 1,38х (руб.) — цена в конце года.
3) 1,38х рублей — это 138% от х рублей.
138% — 100% = 38% — на столько выросла цена за год по отношению к первоначальной цене.
(Ответ: на 38%.)
VIII. Повторение изученного материала
1. № 516 стр. 84 (самостоятельно, устная проверка).
(Ответ: а) х = 0,01; 0,4; 0,354; б) х = 3,5; 4; 4,8; в) х = 4,3; 4,07; 4,96.)
2. Актуализация знаний учащихся.
Сделайте вывод, заполнив пропуски в предложениях:
1) Чтобы найти половину некоторого числа, нужно это число разделить на… или умножить на…
2) Чтобы найти четверть некоторого числа, нужно это число разделить на… или умножить на…
3) Чтобы найти десятую часть некоторого числа, нужно это число разделить на… или умножить на…
4) Чтобы найти сотую часть некоторого числа, нужно это число разделить на… или умножить на…
5) Чтобы найти восьмую часть некоторого числа, нужно это число разделить на… или умножить на…
(Ответ: 1)2; 0,5; 2) 4; 0,25; 3) 10; 0,1; 4) 100; 0,01; 5) 8; 0,125.)
3. Подумайте, как проще найти значение выражения:
3,4 · 0,5; 5,8 · 0,25; 6,4 · 0,125; 500 · 0,2.
IX. Самостоятельная работа
Работа в парах № 495, 499 стр. 81 (смотри алгоритм работы в парах в предыдущем уроке). Привлекать учеников-консультантов для помощи слабым учащимся.
X. Подведение итогов урока
— Сформулируйте правило нахождения дроби от числа.
— Расскажите, как найти часть от числа, выраженного дробью.
Домашнее задание
№ 525, 526, 531 стр. 85; № 534 (б) стр. 86.
