Цели: показать применение переместительного и сочетательного свойства сложения при сложении смешанных чисел; ввести правило сложения смешанных чисел, применять данное правило при нахождении значений выражений, решении задач и уравнений; развивать умение работать самостоятельно с учебником.
Ход урока
I. Организационный момент
II. Анализ контрольной работы
1. Сообщить результаты контрольной работы.
2. Выполнить работу над ошибками, решив задания, в которых допущено много ошибок.
III. Устный счет
1. Найдите значение выражения:
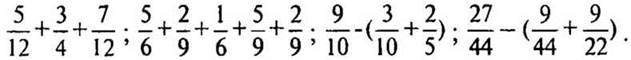
2. Представьте дробную часть чисел в виде неправильной дроби, уменьшив целую часть этих чисел на 1: 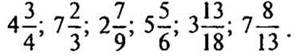
3. Выделите целую часть из чисел: 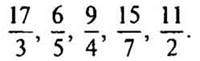
IV. Сообщение темы урока
— Сегодня на уроке мы познакомимся с алгоритмом сложения смешанных чисел.
V. Изучение нового материала
1. Подготовительная работа.
— Назовите смешанные числа:
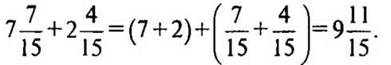
— Почему эти числа так называются?
— Представьте смешанные числа в виде суммы их целой и дробной частей.
— Запишите переместительное свойство сложения в буквенном виде.
а + b = b + а
— Запишите сочетательное свойство сложения в буквенном виде.
(а + b) + с = а + (b + с)
— Приведите примеры на применение этих свойств при сложении дробей. Эти свойства позволяют складывать смешанные числа.
2. Работа над новой темой.
а) Сложите числа: 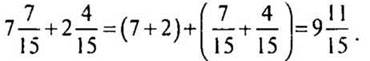
— Расскажите, как складываются смешанные числа, когда дробные части имеют одинаковые знаменатели. (Сначала складывают целые части, затем — дробные части.)
— Какие свойства сложения были использованы? (Сочетательное и переместительное.)
б) Сложите числа: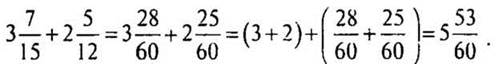
— Что делать, когда дробные части смешанных чисел имеют разные знаменатели?
(По ходу ответов учащихся учитель на доске может записать памятку сложения смешанных чисел, затем эту памятку дети записывают в тетрадь).
3. Работа с учебником, стр. 59 (в парах).
— Рассмотрите в учебнике пример 1.
— Сложите числа:
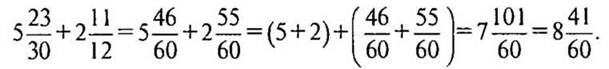
— Как поступить в том случае, когда дробная часть 101/60 представлена неправильной дробью? (Выделишь целую часть.)
4. Работа с учебником, стр. 60 (в парах).
— Рассмотрите в учебнике пример 2.
— Прочитайте правило сложения смешанных чисел.
— Расскажите это правило товарищу.
— Приведите свои примеры, аналогичные примерам 1 и 2 учебника.
VI. Закрепление изученного материала
№ 376 стр. 61 (с подробным комментированием у доски и в тетрадях, первые два примера записать подробно, потом короче).
Образец решения:
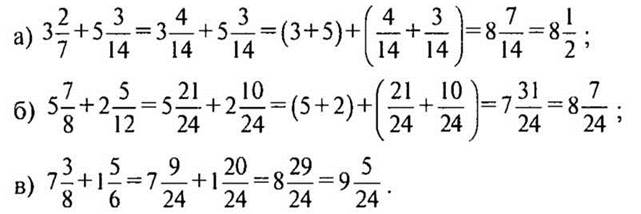
(Ответы: 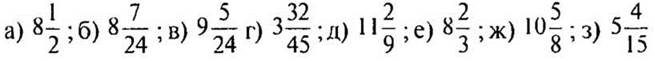 .)
.)
VII. Физкультминутка
VIII. Работа над задачей
1. № 382 стр. 62 (у доски ученик во время разбора задачи записывает решение).
— Прочитайте задачу. Что известно? Что надо узнать?
— Давайте решим задачу с вопросами по действиям.
— Примем за единицу весь бассейн.
— Зная, что весь бассейн это — 1, или целое, и что первая труба, работая отдельно, заполняет его за 4 ч, первым действием можно узнать, какую часть бассейна заполняет первая труба за 1 ч.
Решение:
Пусть 1 – весь бассейн.
Какую часть бассейна заполняет первая труба за 1 ч? 1/4 (часть)
Какую часть бассейна заполняет вторая труба за 1 ч? 1/6 (часть)
Какую часть бассейна заполняют обе трубы за 1 ч, работая одновременно?
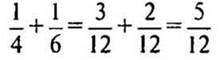 (частей бассейна.)
(частей бассейна.)
Какую часть бассейна останется наполнить после 1 ч совместной работы двух труб?
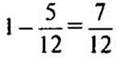 (частей бассейна.)
(частей бассейна.)
(Ответ: 7/12 частей бассейна.)
2. № 389 стр. 63 (один ученик на обратной стороне доски, остальные — самостоятельно, самопроверка).
— Что такое периметр треугольника?
— Запишите формулу для нахождения периметра треугольника ABC.
Решение:
Р = АВ + ВС + АС
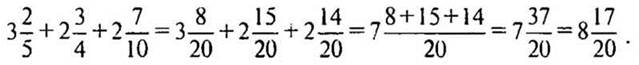
(Ответ: периметр треугольника — 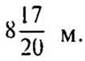 )
)
IX. Самостоятельная работа
Вариант I. № 408 (1 строчка) стр. 65.
Вариант II. № 408 (2 строчка) стр. 65.
X. Подведение итогов урока
— На каких свойствах сложения основано сложение смешанных чисел.
— Расскажите алгоритм сложения смешанных чисел.
Домашнее задание
№ 414 (а—г), 416 (а, б) стр. 66; № 418, 425 (а) стр. 67. По желанию № 287 стр. 47.














