Цели: повторить правило сравнения дробей с одинаковыми знаменателями, правило нахождения дополнительного множителя, правило сложения и вычитания дробей с одинаковым знаменателем; вывести правила сложения и вычитания дробей с разными знаменателями; научить применять эти правила при решении примеров и задач; развивать математическую речь.
Информация для учителя
На первых уроках целесообразно выполнять подробную запись решения, проговаривая каждое действие, потом можно перейти к краткой записи.
При сложении и вычитании дробей лучше над дробями подписывать дополнительный множитель. В результате действий должна получаться несократимая дробь или смешанное число, где дробная часть представлена в виде несократимой дроби.
Показать учащимся, что переместительное и сочетательное свойства сложения, свойства вычитания и свойства нуля действительны и для дробей. Их применяют для упрощения вычислений.
Обратить внимание учащихся на удобный порядок выполнения действий, когда складывают более двух дробей.
Ход урока
I. Организационный момент
II. Актуализация знаний учащихся
1. Ознакомить учащихся с результатами самостоятельной работы.
2. Дать индивидуальные карточки учащимся, разрешив воспользоваться записями в классной тетради.
III. Устный счет
1. От ленты длиной 2/3 м нужно отрезать 1/2 м. Как это сделать, не пользуясь линейкой?
Решение:
1) Привести дроби к общему знаменателю 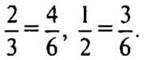
2) Наша лента длиной 2/3 м разделена на 4 равные части, а нам, чтобы отрезать 1/2 м, нужно взять 3 такие части.
3) Для этого складываем ленту пополам, затем опять пополам. Берем 3 равные части — это и будет 1/2 м.
2. Как из целого вычесть часть?
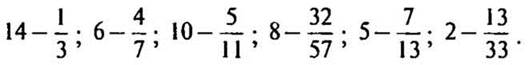
3. Выразите неизвестные переменные:
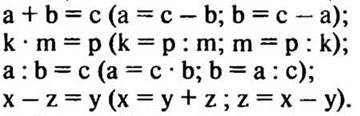
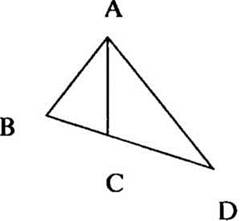
4. Сосчитайте количество треугольников на чертеже. (3.) Назовите эти треугольники.
5. На веточке сирени 35 цветков, у которых по 4 или по 5 лепестков. Всего лепестков 153.
Сколько цветков с 5 лепестками? (Если бы каждый цветок состоял из 4 лепестков, то лепестков было бы 140. Лишние 13 лепестков принадлежат 13 цветкам с 5 лепестками.)
IV. Индивидуальная работа
1 карточка
1. Запишите дроби в порядке возрастания: 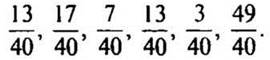
2. Сравните дроби: 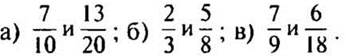
3. Приведите к наименьшему общему знаменателю дробные части чисел: 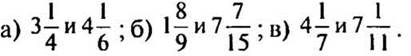
2 карточка
1. Запишите дроби в порядке убывания: 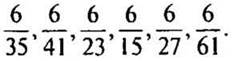
2. Сравните дроби: 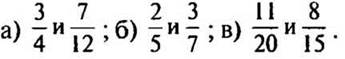
3. Приведите к наименьшему общему знаменателю дробные части чисел: 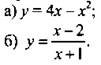
V. Сообщение темы урока
VI. Изучение нового материала
1. Работа над новой темой.
— Приведите дроби 3/4 и 1/3 к НОЗ.
— Выполните действия с полученными дробями:
а) сравните дроби;
б) найдите сумму дробей;
в) найдите разность дробей.
— Обобщите решения и сформулируйте правила сравнения, сложения и вычитания дробей с разными знаменателями.
2. Работа с учебником.
— Прочитайте пример 4 на стр. 49.
— Найдите значение выражений: 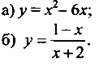
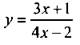
— Как это удобнее сделать? (Сгруппировать дроби, имеющие одинаковые знаменатели.)
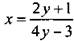
VII. Закрепление изученного материала
№ 319 (а—е) стр. 52 (с подробным комментированием у доски и в тетрадях).
Решение:
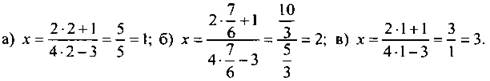
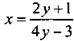
— Для решения примера д) мы применили свойство нуля. Сформулируйте его.
— Запишите это свойство в буквенном виде:
а + 0 – а
а – 0 = а
а – а = 0
VIII. Физкультминутка
IX. Работа над задачей
№ 356 (1) стр. 56 (самостоятельно после разбора).
Это задача на движение вдогонку.
— Что нужно знать, чтобы ответить на вопрос задачи? (Все расстояние между двумя самолетами, то есть на сколько больше второй самолет пролетит, чем первый, и скорость удаления.)
— Что нужно знать, чтобы найти скорость удаления? (Скорость двух самолетов.)
— Что нужно знать, чтобы найти, на сколько больше второй самолет пролетит, чем первый? (Знать расстояние, которое было между двумя самолетами через 0,5 ч после вылета первого, и расстояние, на которое второй самолет будет впереди.)
Решение:
1) 600 · 0,5 = 300 (км) — пролетит первый самолет за 0,5 ч.
2) 750 — 600 = 150 (км/ч) — больше скорость второго самолета, чем первого или скорость удаления.
3) 300 + 225 = 525 (км) – на столько больше километров должен пролететь второй самолет.
4) 525: 150 = 3,5 (4).
(Ответ: через 3,5 ч второй самолет будет впереди первого после своего вылета.)
X. Самостоятельная работа
(Самопроверка, решение на доске.)
№ 335, 336, 337 стр. 54.
— Кто не понимает, как решать задачу, подойдите ко мне. (Учитель подробно разбирает решение задач, записывая его на обратной стороне доски.)
XI. Закрепление изученного материала
1. № 307 (б) стр. 50 (у доски на обратной стороне и в тетрадях).
— Как сравнивать дроби с разными знаменателями?
— Чему равен НОЗ всех дробей? (НОЗ этих дробей равен 24, так как 24 кратно всем остальным знаменателям.)
Решение:
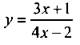
5/24 к новому знаменателю приводить не надо 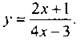
(Ответ: 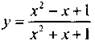 )
)
2. № 353 стр. 56 (у доски и в тетрадях).
— Какая дробь называется правильной?
— Как перевести в правильную дробь?
(Ответ: 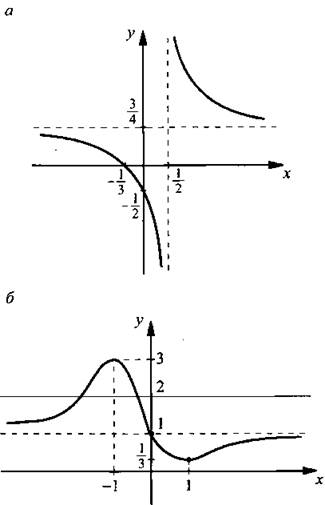 )
)
XII. Подведение итогов урока
— Расскажите, как складывают и вычитают дроби с разными знаменателями.
— Что значит записать дроби в порядке убывания?
— Сравните дроби: 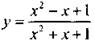
Домашнее задание
Учебник стр. 52 (прочитать текст под рубрикой «Говори правильно»).
№ 360 (а-з), 363 стр. 57; № 372 стр. 58.














