Цели: отрабатывать умение сокращать дроби; закреплять умение решать задачи на движение по воде; расширять кругозор и математическую культуру учащихся; развивать умение самостоятельно работать.
Ход урока
I. Организационный момент
II. Устный счет
1. Найдите наибольший общий делитель и наименьшее общее кратное чисел: 25 и 40; 55 и 60; 4 и 15; 8 и 36; 18 и 72; 15 и 60; 9 и 12; 45 и 60.
2. Сократите дроби: 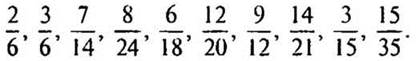
3. Выразите неизвестные переменные: ![]()
Эти вопросы (можно выборочно) задаются в том случае, если учащиеся допустили много ошибок:
— Как называются числа при сложении? (1 слагаемое, 2 слагаемое, сумма.)
— Как они между собой взаимосвязаны? (Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.)
— Как называются числа при вычитании? (Уменьшаемое, вычитаемое, разность.)
— Как они между собой взаимосвязаны? (Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое; чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.)
— Как называются числа при делении? (Делимое, делитель, частное.)
— Как они между собой взаимосвязаны? (Чтобы найти неизвестное делимое, надо частное умножить на делитель; чтобы найти неизвестный делитель, надо делимое разделить на частное.)
— Как называются числа при умножении? (1 множитель, 2 множитель, произведение.)
— Как они между собой взаимосвязаны? (Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.)
4. Какую цифру надо поставить вместо * в числах 342*, * 245, 1* 48*, * 987*, чтобы они делились: а) на 2; б) на 5; в) на 10; г) на 3; д) на 9.
5. Угадайте корень уравнения:
а) 4х + х · х = 45;
б) 5х + х · х – 50;
в) 4х – х · х = 0;
г) 6х – х · х = 8.
III. Сообщение темы урока
— Роджер Бэкон говорил о математике: «…дверь и ключ к науке». Без математических знаний человек не может сформироваться как гармоническая личность. Поэтому давайте продолжим с вами осваивать математику, каждый день добывая новые и новые знания, которые помогут в изучении других предметов и в нашей практической жизни.
IV. Изучение нового материала
а) Сократите дробь 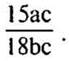
— Числитель дроби представлен в виде произведения трех чисел 15, а и с, а знаменатель — 18, b, с.
— Назовите общий делитель числителя и знаменателя. (3 с.)
б) Сократите дроби: 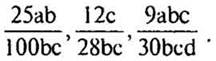
— Назовите общий делитель числителя и знаменателя дроби.
V. Физкультминутка
VI. Закрепление изученного материала
1. — Какая дробь называется несократимой?
— Приведите примеры.
№ 243 (б) стр. 39 (один ученик работает на обратной стороне доски, а остальные самостоятельно в тетрадях, затем самопроверка).
— Дроби можно сокращать любым удобным способом.
(Ответ: 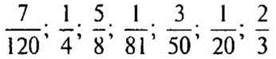 .)
.)
— Что называют сокращением дробей?
2. № 244 (б) стр. 40 (самостоятельно, взаимопроверка).
На доске записаны ответы.
(Ответы: 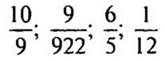 .)
.)
3. Выразите в часах: 1 мин; 15 мин; 25 мин; 38 мин; 4 мин; 12 мин; 30 мин.
4. № 246 стр. 40 (после краткого разбора самостоятельно, с последующей проверкой).
— Какой угол называется развернутым? (Угол, градусная мера которого равна 180°, называется развернутым.)
VII. Самостоятельная работа
Вариант I
1. Сократите дроби: 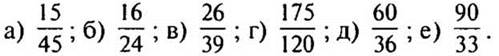
2. Сколько десятых, пятнадцатых, двадцатых, сотых долей содержится в дроби 4/5?
Вариант II
1. Сократите дроби: 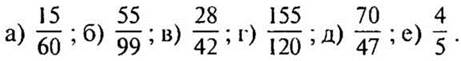
2. Сколько десятых, пятнадцатых, двадцатых, сотых долей содержится в дроби 2/5?
VIII. Работа над задачей
1. Составьте задачу о движении по воде по краткой записи.
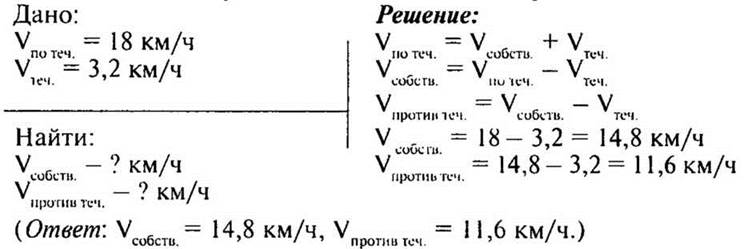
2. № 267 (2) стр. 42.

IX. Повторение изученного материала
1. № 255 стр. 41 (устно).
— Какие числа называются взаимно простыми?
(Ответ:
1 и 3, 1 и 10, 1 и 12, 1 и 13, 1 и 15, 1 и 16, 1 и 39,
3 и 10, 3 и 13, 3 и 16,
10 и 13, 10 и 39,
12 и 13,
13 и 15, 13 и 16,
15 и 16,
16 и 39.)
2. № 257 стр. 41 (самостоятельно).
(Ответ:
а) m = 15,
б) х = 20,
в) а = 1, b = 9; а = 9, b = 1; а = 3, b = 3;
г) х = 1, у = 14; х = 14, у = 1; х = 2, у = 7.)
3. № 249 стр. 40 (устно).
— Вспомните, как складываются и вычитаются дроби с одинаковыми знаменателями.
(Ответ: 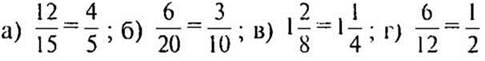 .)
.)
X. Подведение итогов урока
— В каком случае дробь a/b будет несократимой? (Когда числа а и b будут взаимно простые.)
— Приведите примеры сократимых дробей.
Домашнее задание
№ 268 (б) стр. 42; № 271, 274 (б) стр. 43; № 264 стр. 42.
По желанию, на стр. 41 учебника прочитать исторический материал о фигурных числах.














