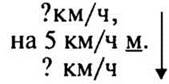Цели: отрабатывать умения решать задачи с помощью уравнений, уравнения; обобщение и закрепление знаний по теме «Раскрытие скобок. Подобные слагаемые»; подготовить учащихся к контрольной работе.
Ход урока
I. Организационный момент
II. Устный счет
1. Раскройте скобки:

2. При каких значениях а верно неравенство:
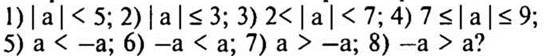
3. Решите уравнения:
1) (y – 7)(у + 2) = 0;
2) (х + 10)(х – 1) = 0;
3) (с – 6)(с – 9) = 0;
4) (b + 3)(с + 4) = 0.
4. Часы со стрелками отстают на 6 мин каждый день. Через сколько дней они будут показывать опять верное время?
5. Два числа и их произведение оканчиваются одной и той же цифрой. Какова эта цифра, если сумма трех таких цифр больше 15? (6.)
III. Индивидуальная работа (для более подготовленных учащихся)
Задание можно не переписывать.
1 карточка
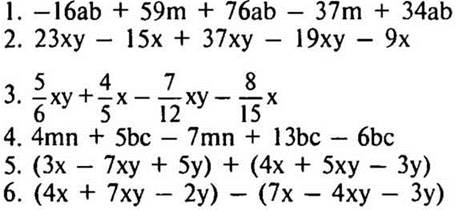
2 карточка
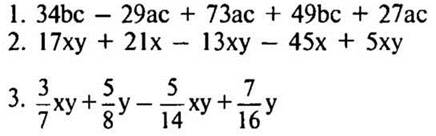
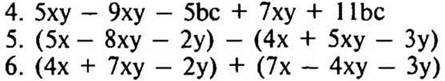
IV. Сообщение темы урока
— Сегодня мы будем готовиться к контрольной работе.
V. Закрепление изученного материала
1. № 1282 (ж—и) стр. 225 (один ученик решает на обратной стороне доски, остальные — в тетрадях, взаимопроверка).
Решение:
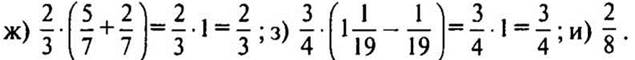
2. № 1284 (е—к) стр. 225 (самостоятельно, взаимопроверка).
— Сколько групп подобных слагаемых в первом выражении? (3.)
Решение:
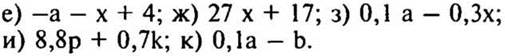
VI. Работа над задачей
№ 1289 стр. 226 (у доски и в тетрадях).
— Прочитайте задачу.
— Что известно? Что надо узнать?
— Сделайте краткую запись в виде таблицы.
— Какие слова нужны для составления краткой записи?
|
|
Скорость |
Время |
Расстояние |
|
Пешком
Велосипед |
|
3ч
4ч |
|
Пусть х (км/ч) – скорость туриста пешком; х — натуральное число.
|
|
Скорость |
Время |
Расстояние |
|
Пешком Велосипед |
х х + 5 |
3ч 4ч |
3ч 4(х + 5) |
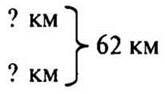
1) Зная, что весь путь 62 км:
3х + 4(х + 5) = 62
3х + 4х + 20 = 62
7х = 62 – 20
7х = 42
х = 42 : 7
х = 6; 6 (км/ч) — скорость туриста пешком.
2) 6 + 5 = 11 (км/ч) — скорость туриста на велосипеде.
(Ответ: 6 км/ч и 11 км/ч.)
VII. Физкультминутка
VIII. Повторение изученного материала
1. На чем основано раскрытие скобок?
— Найдите значение выражения:
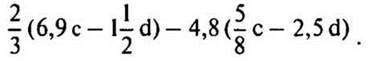
Решение:
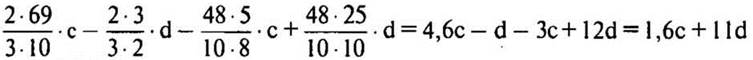
2. № 1294 (в, г) стр. 227 (устно).
— Расскажите, как удобнее найти значение выражения.
Решение:
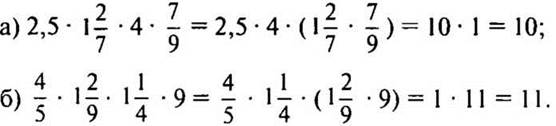
IX. Самостоятельная работа (10 мин)
Вариант I
1. Решите уравнение:
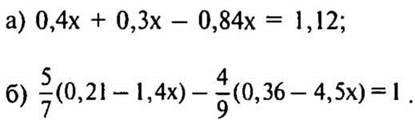
2. Турист проехал на поезде и на теплоходе 605 км. Средняя скорость поезда 60 км/ч, а теплохода 25 км/ч. Сколько времени турист ехал на поезде и сколько на теплоходе, если известно, что на теплоходе он ехал на 3 ч меньше, чем на поезде?
3. Найдите значение выражения 5k — (3k — 8р), если k + 4р = 17.
Вариант II
1. Решите уравнение:
а) 0,7х — 0,4х — 0,98х = 12,73;
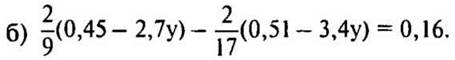
2. Велосипедист ехал по шоссе со скоростью 14 км/ч, а по грунтовой дороге — 8 км/ч. Всего он проехал 11,6 км. Сколько времени он ехал по шоссе и сколько по грунтовой дороге, если но грунтовой дороге он ехал на 0,2 ч меньше, чем по шоссе?
3. Найдите значение выражения -2m – (6n – 5m), если m – 2n = – 12.
X. Подведение итогов урока
— Какие слагаемые называют подобными?
— Приведите примеры подобных слагаемых.
Домашнее задание
№ 1304 (д, е), 1305 (д, е), 1306 (и—м), 1307 (ж, з) стр. 228, № 1310 стр. 229.