Цели: показать учащимся, что свойства сложения и умножения, известные для неотрицательных чисел, справедливы для любых рациональных чисел; способствовать развитию творческого мышления; формирование навыков самоконтроля; воспитание аккуратности, культуры учебного труда.
Ход урока
I. Организационный момент
II. Устный счет
1. Решите уравнения: 1) 0 : х = 0; 2) у : 0 = 6 (Не имеет смысла, так как делить на 0 нельзя.); 3) 6 : х = 6; 4) у : 6 = 6.
2. Переведите 20%, 13%, 5%, 10%, 75%, 4% в десятичные дроби.
3. Какую часть года составляют 1 месяц, 4 месяца, 6 месяцев, 8 месяцев, 10 месяцев?
4. Одно число меньше другого в 5 раз. Их сумма равна 54. Найдите эти числа.
5. Число 666 требуется увеличить в полтора раза, не производя над этим числом никаких арифметических действий. Как это сделать? (Лист, на котором написано число, перевернуть на 180°, получится число 999.)
III. Индивидуальная работа
1 карточка
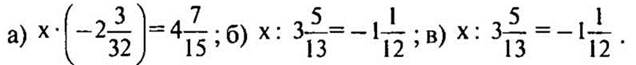
2 карточка
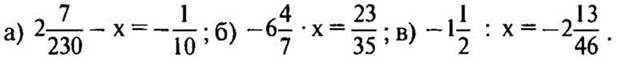
IV. Сообщение темы урока
V. Изучение нового материала
1. Подготовительная работа.
— Какие числа называют рациональными? Приведите примеры.
— В каком виде можно записать любое рациональное число?
2. Работа над новой темой.
— Свойства сложения и умножения натуральных чисел, обыкновенных дробей также верны и для рациональных чисел.
Для любых рациональных чисел а, b, с:
— Переместительное свойство сложения а + b = b + а.
— Сочетательное свойство сложения (а + b) + с = а + (b + с).
— Свойство нуля а + 0 = 0 + а = а.
— а + (-а) = 0.
— Переместительное свойство умножения а · b = b · а.
— Сочетательное свойство умножения (а · b) · с = а · (b · с).
— Свойство нуля а · 0 = 0 · а = 0.
— Свойство 1 а · 1 = 1 · а = а.
— Если а ≠ 0, 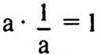
— Распределительное свойство умножения относительно сложения (а + b) · с = а · с + b · с.
— При каких значениях а и b верно равенство а · b = 0?
— Произведение двух множителей может быть равно нулю лишь в том случае, когда хотя бы один из множителей равен нулю.
— Если а · b = 0, то либо а = 0, либо b = 0.
— Возможен случай, что а = 0 и b = 0.
VI. Закрепление изученного материала
1. № 1201 стр. 208 (на доске и в тетрадях).
Решение:
— От перестановки слагаемых значение суммы не меняется.
а + b = b + а
при а = 0,7; b = 1,2: 0,7 + 1,2 = 1,9; 1,2 + 0,7 = 1,9;
при 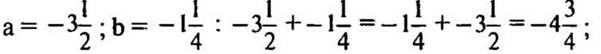
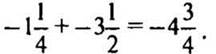
2. № 1202 стр. 208 (с подробным комментированием на доске и в тетрадях).
Решение:
— Сумма нескольких слагаемых не зависит от порядка действий.
(а + b) + с = а + (b + с)
При а = -0,7; b = -0,3; с = 1,2:
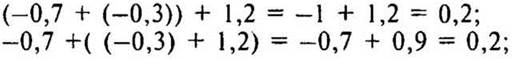
При 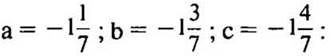
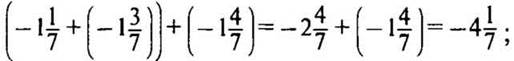
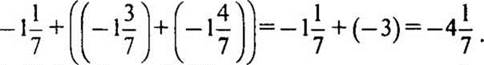
3. № 1203 стр. 208 (на доске и в тетрадях).
Решение:
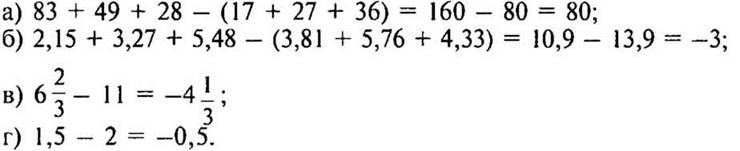
4. № 1204 стр. 208 (на доске и в тетрадях).
— Чему равна сумма противоположных чисел? (Нулю.)
(Ответ: 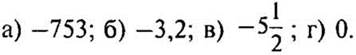 )
)
VII. Физкультминутка
VIII. Повторение изученного материала
1. Составьте программу действий: ![]()
2. № 1217 стр. 210 (самостоятельно, устная проверка).
— Что называют модулем числа?
— Может ли модуль быть равен отрицательному числу? {Нет.)
— Модуль какого числа равен нулю? (Нуля.)
(Ответ: а) х = 5,2; х = —5,2; б) нет корней; в) у = 0.)
IX. Работа над задачей
Сливки составляют 0,1 массы молока, а сливочное масло составляет 0,3 массы сливок. Сколько сливочного масла можно получить из суточного надоя коровы, равного 15 кг молока?
(По мере выяснения вопросов учитель составляет краткую запись условия задачи на доске.)
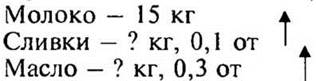
— Сколько молока имеется по условию задачи?
— Какую часть всего молока составляют сливки? Что хотят получить из сливок?
— Какая часть массы сливок приходится на сливочное масло?
— Что требуется узнать в задаче? Главный вопрос задачи обведите в кружок.
— Решите задачу двумя способами.
— Разобрать план решения каждым способом.
(Дети решение записывают сами, а затем проверяют его по образцу (один ученик решает на обратной стороне доски).)
Решение:
1 способ
1) 15 · 0,1 = 1,5 (кг) — сливок в 15 кг молока.
2) 1,5 · 0,3 = 0,45 (кг) — масса сливочного масла.
2 способ
1) 0,1 · 0,3 = 0,03 — массы молока составляет масло.
2) 15 · 0,03 = 0,45 (кг) — масса сливочного масла.
(Ответ: 0,45 кг.)
Доска бела от мела,
Рука устала, затекла спина,
Мы друг на друга смотрим очумело,
А все-таки задача решена!
Додумались! Добились! «Раскололи»!
Намаялись, однако же смогли!
Забыли о кино и о футболе
Звонку не рады — до чего дошли.
X. Самостоятельная работа (10 мин)
Вариант I
1. Найдите значение выражения:
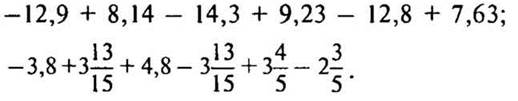
2. Упростите выражение: 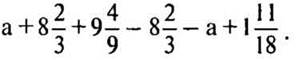
3. Выразите числа 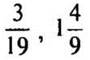 в виде приближенного значения десятичной дроби до сотых.
в виде приближенного значения десятичной дроби до сотых.
4. Представьте в виде обыкновенной дроби число 0,(2).
Вариант II
1. Найдите значение выражения:
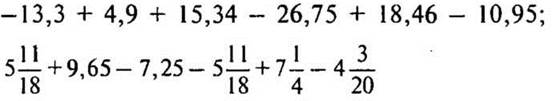
2. Упростите выражение: 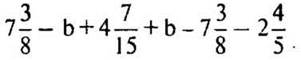
3. Выразите числа 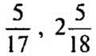 в виде приближенного значения десятичной дроби до тысячных.
в виде приближенного значения десятичной дроби до тысячных.
4. Представьте в виде обыкновенной дроби число 0,(4).
XI. Подведение итогов урока
— Назовите свойства нуля и единицы.
— Чему равна сумма противоположных чисел?
— Чему равно произведение числа на обратное ему число?
Домашнее задание
№ 1226 (а, б), 1227 (а, б), 1228 стр. 212; № 1230 стр. 213. По желанию № 1233 (а).














