Цели: отрабатывать умение записывать числа в виде a/n, где а — целое число, а n — натуральное число; выражать числа в виде десятичных или периодических дробей; развивать навыки устного счета, внимание, память; воспитывать серьезное отношение к учебному труду.
Ход урока
I. Организационный момент
II. Устный счет
1. Выполните действия:
5 · (-1); 0 : (-4,6); -2,34 · 0; -3,5 · (-1); -32 : 0.
— Какое выражение не имеет смысла? Почему? (Делить на нуль нельзя.)
2. Кто быстрей?
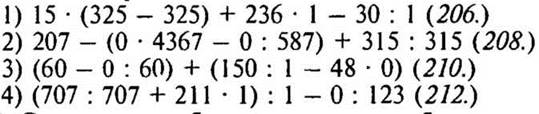
3. Сколько потребуется времени, чтобы поезд, длина которого 0,5 км, идущий со скоростью 60 км в час, прошел тоннель длиной в 0,5 км? (/ мин.)
4. Если в 12 часов ночи идет дождь, то можно ли ожидать, что через 72 часа будет солнечная погода? (Нет, так как будет ночь.)
5. Хорошо известно, что пять в квадрате — 25, десять в квадрате — 100, половина в квадрате – 1/4, треть в квадрате — 1/9. А чему равен угол в квадрате? (90°.)
III. Индивидуальная работа
1 карточка
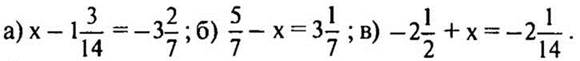
2 карточка
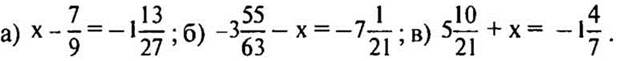
IV. Сообщение темы урока
— Сегодня на уроке мы будем учиться записывать любое рациональное число в виде десятичной дроби или в виде периодической дроби, узнаем, что значит округление числа с избытком и с недостатком.
V. Изучение нового материала
1. Подготовительная работа.
— Запишите в виде десятичных дробей:
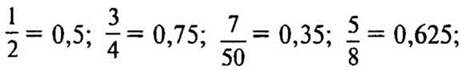
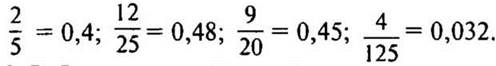
2. Работа над новой темой.
Вы знаете, что не все обыкновенные дроби можно представить в виде десятичной дроби.
— Давайте проверим, можно ли записать дроби в виде десятичных дробей:
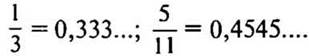
В данных записях одна или несколько цифр бесконечно много раз повторяются. Такие записи называют периодическими дробями.
Пишут 0,333… = 0,(3); 0,4545… = (0,45).
— Любое рациональное число можно записать в виде десятичной дроби (в частности, целого числа), либо в виде периодической дроби.
3. Работа с учебником.
— Самостоятельно прочитайте два последних абзаца пункта 37 в учебнике на стр. 203.
— Какое число является приближенным значением до десятых с недостатком для дроби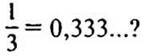 
(0,3.)
— А приближенным значением до десятых с избытком для этой же дроби? (0,4.)
Округлим число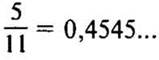 
до десятых: 
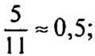до сотых: 
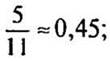до тысячных: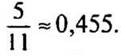 
— В каком случае округлили с недостатком, а в каком с избытком?
— Прочитайте текст в учебнике на стр. 192 под рубрикой «Говори правильно».
VI. Закрепление изученного материала
1. № 1180 стр. 204 (на доске и в тетрадях).
(Ответ: 0,(5); 0,58(3); 5,52; 4,4(6); 0,675; 3,2(7); 1,12; 0,1(6).)
2. № 1181 стр. 204 (на доске и в тетрадях).
(Ответ: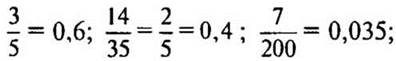 
)
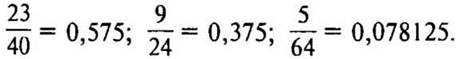3. № 1182 стр. 204 (на доске и в тетрадях).
— Как проверить, верны ли равенства? (Выполнить деление.) (Ответ: все равенства верны.)
4. № 1183 стр. 205 (с подробным комментированием на доске и в тетрадях).
(Ответ: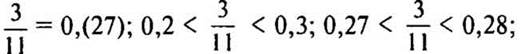 
)
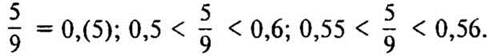VII. Работа над задачей
№ 1078 (б, г, е, з) стр. 183 (самостоятельно, устная проверка).
— Записать только уравнение, устно обосновать ответ.
Решение:
б) х + х – 0,2 = 2,4;
г) х + 1,5 х = 2,4;
е) х + 0,2 х = 2,4;
з) х + 1,4 х = 2,4.
VIII. Самостоятельная работа (10 мин)
Вариант I
1. Выразите в виде десятичной или периодической дроби числа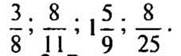 
2. Выразите числа в виде приближенного значения десятичной дроби до тысячных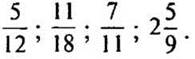 
Вариант II
1. Выразите в виде десятичной или периодической дроби числа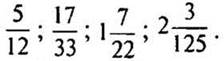 
2. Выразите числа в виде приближенного значения десятичной дроби до тысячных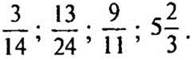 
IX. Подведение итогов урока
— В каком виде можно записать любое рациональное число?
— Какая запись числа называется периодической дробью?
— Какими числами является сумма, разность, произведение рациональных чисел?
— Всегда ли частное двух рациональных чисел является рациональным числом?
Домашнее задание
Учебник, стр. 204 (прочитать текст под рубрикой «Говори правильно».)
№ 1197 стр. 206, № 1198, 1199, 1200 (б) стр. 207.
