Цели: ввести понятие рационального числа; учить записывать числа в виде рациональных чисел; обобщить знания учащихся по теме «Умножение и деление рациональных чисел»; совершенствовать вычислительные навыки учащихся; развивать любознательность, активность.
Ход урока
I. Организационный момент
II. Устная контрольная работа
Вариант I
Вариант II
III. Индивидуальная работа
1 карточка
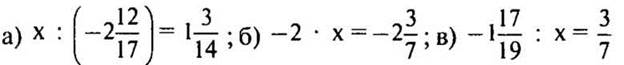
2 карточка
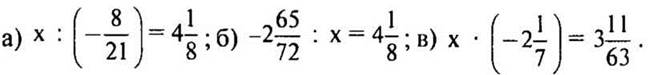
IV. Сообщение темы урока
— Сегодня на уроке мы познакомимся с рациональными числами, будем учиться записывать числа в виде рациональных чисел.
V. Изучение нового материала
1. Подготовительная работа.
— Распределите по группам числа:
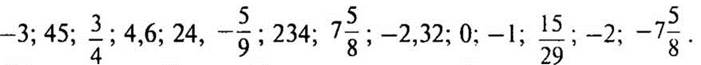
(Целые — дробные, обыкновенные дроби — десятичные дроби, положительные — отрицательные, обыкновенные дроби — смешанные числа, натуральные числа — остальные числа.)
2. Работа над новой темой.
Определение. Число, которое можно записать в виде отношения a/n, где а — целое число, а n — натуральное число, называют рациональным числом.
1. Любое целое число является рациональным, так как его можно записать в виде a/1:
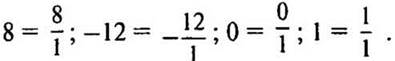
2. Любая отрицательная дробь будет рациональным числом, так как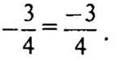 
3. Любая десятичная дробь тоже является рациональным числом, так как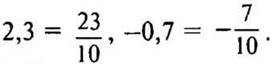 
4. Сумма, разность и произведение рациональных чисел тоже рациональное число.
5. Частное двух чисел, если делитель отличен от нуля, тоже рациональное число.
VI. Закрепление изученного материала
1. № 1178 стр. 204 (на доске и в тетрадях).
— Какие числа называют рациональными?
2. № 1179 стр. 204 (на доске и в тетрадях).
— Что надо сначала сделать, чтобы суммы представить в виде a/n?
(Найти значение каждой суммы.)
VII. Повторение изученного материала
1. № 1187 стр. 205 (устно).
— Можно привести примеры, записать их на доске.
(Ответ: a) m ≥ 0; б) m < 0; в) m < 0 ; г) m > 0; д) m = 0; е) m ≤ 0; ж) m > 0; з) m < 0.)
2. № 1188 стр. 205 (устно).
(Ответ: равенство будет верным, если а = b; приведем контрпример: а = 1, b = 2: 1 : 2 = 2 : 1 – неверно.)
3. № 1191 стр. 206 (самостоятельно, устная проверка).
— Что значит привести дробь к новому знаменателю?
— На чем основано приведение дроби к новому знаменателю? (На основном свойстве дроби.)
— Что такое дополнительный множитель? (Число, на которое множат и числитель, и знаменатель.)
— Как найти дополнительный множитель? (Надо новый знаменатель разделить на старый, частное и будет дополнительным множителем.)
(Ответ: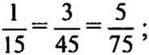 
к остальным знаменателям дробь привести нельзя, так как они не кратны 15.)
VIII. Физкультминутка
IX. Работа над задачей
№ 1141 (г) стр. 194 (на обратной стороне доски и в тетрадях, взаимопроверка).
— Прочитайте задачу.
— Решите самостоятельно алгебраическим способом.
1) Пусть х (м) — высота сосны,
0,4х (м) – высота ели.
Так как сосна выше ели на 1,2 м, то
х — 0,4х = 1,2; 0,6х = 1,2; х = 12 : 6; х = 2.
2 (м) — высота сосны.
2) 2 — 1,2 = 0,8 (м) — высота ели.
(Ответ: ель 0,8 м, сосна 2 м.)
X. Самостоятельная работа (10 мин)
Вариант I
Покажите, что числа являются рациональными:
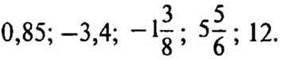
Вариант II
Покажите, что числа являются рациональными:
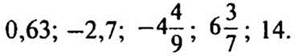
XI. Подведение итогов урока
— Какие числа называют рациональными?
— Покажите, что любое целое число является рациональным числом.
— Покажите, что любая десятичная дробь является рациональным числом.
Домашнее задание
Учебник, стр. 204 (прочитать текст под рубрикой «Говори правильно».
№ 1175 стр. 201; № 1196 стр. 206; № 1200 (а) стр. 207.
