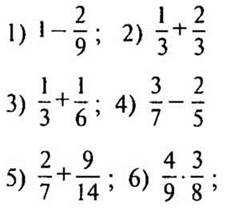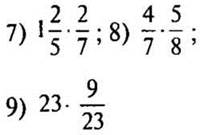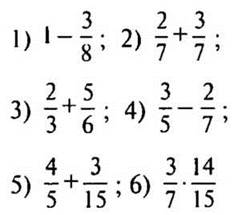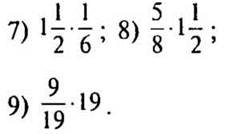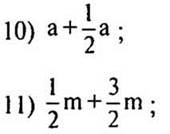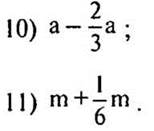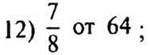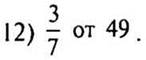Цели: ввести понятие взаимно обратных чисел; формировать навык умножения дробей; отрабатывать умение решать уравнения нового типа; развивать внимательность, логическое мышление.
Ход урока
I. Организационный момент
«Гений состоит из одного процента вдохновения и 99 процентов потения». (Эдисон)
— Что это значит?
II. Анализ контрольной работы
1. Ознакомить учащихся с результатами контрольной работы.
2. Решить задания, в которых допущено наибольшее количество ошибок.
III. Устная контрольная работа
Ученики записывают под копирку ответы под соответствующим номером. Первый листок сдается учителю. Проверку осуществить способом взаимопроверки.
|
Вариант I |
Вариант II |
|
1—9. Вычислите: |
|
|
|
|
|
10—11. Упростите выражение: |
|
|
|
|
|
12. Найдите: |
|
|
|
|
(Ответы:
Вариант I
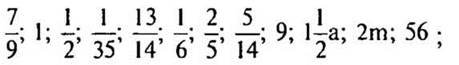
Вариант II
 )
)
Критерии оценок:
«5» — нет ошибок.
«4» — 1—2 ошибки.
«3» — 3—4 ошибки.
«2» — более 4 ошибок.
IV. Сообщение темы урока
— Сегодня на уроке вы познакомитесь с новым понятием взаимно обратных чисел.
V. Изучение нового материала
1. Подготовительная работа.
— Какие числа называются взаимно простыми? (Натуральные числа называются взаимно простыми, если их НОД равен 1.)
— Приведите примеры взаимно простых чисел. (HОД(3; 7) = 1, следовательно, 3 и 7 — взаимно простые числа и т. д.)
2. Работа над новой темой.
— Выполните умножение:
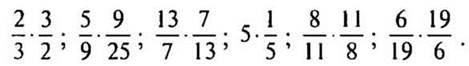
— Какое произведение лишнее? Почему?
Определение. Два числа, произведение которых равно 1, называют взаимно обратными.
— Приведите примеры взаимно обратных чисел.
— Как записать число, обратное числу a/b? (b/a.)
— Какие условия должны соблюдаться для чисел a, b? (а ≠ 0, b ≠ 0)
Запись в тетрадях:
 — взаимно обратные числа, так как
— взаимно обратные числа, так как 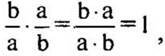 а ≠ 0, b ≠ 0.
а ≠ 0, b ≠ 0.
— Найдите число, обратное данному числу: 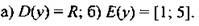
Решение:
а) 10;
б) Как вы думаете, в каком виде надо сначала записать число 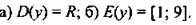 (В виде неправильной дроби.)
(В виде неправильной дроби.)
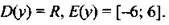 следовательно, обратным числу
следовательно, обратным числу ![]() будет число 5/12.
будет число 5/12.
в) 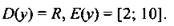 следовательно, обратным числу 0,5 будет число 2.
следовательно, обратным числу 0,5 будет число 2.
VI. Закрепление изученного материала
1. № 577 (а—в) стр. 94 (с подробным комментированием у доски и в тетрадях).
— Как доказать, что данные числа являются взаимно обратными? (Выполнить умножение, если произведение этих чисел равно 1, то числа являются взаимно обратными.)
(Ответ: г) да; б) нет; в) да.)
2. № 580 стр. 95 (подробным комментированием у доски и в тетрадях).
— Что неизвестно в уравнении? (Второй множитель.)
— Как найти неизвестный множитель? (Произведение разделить на известный множитель.)
— Возникла проблема: мы не умеем делить на дробные числа. Как по-другому можно решить это уравнение? (Так как произведение равно единице, то второй множитель будет являться числом, обратным первому множителю.)
Решение уравнений д) и е) основано на свойстве единицы при умножении.
(Ответ: 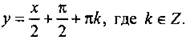 )
)
VII. Физкультминутка
VIII. Работа над задачей
№ 589 стр. 96 (с подробным комментированием у доски и в тетрадях).
— Прочитайте задачу.
— Что такое среднее арифметическое нескольких чисел?
— Что известно?
— Что надо найти?
— Запишем краткую запись.
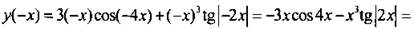 среднее арифметическое — 3,1
среднее арифметическое — 3,1
1) Пусть х — 1 число,
х + 0,9 — 2 число,
2 х — 3 число.
Зная, что среднее арифметическое трех чисел равно 3,1, составим и решим уравнение:
(х + х + 0,9 + 2 х) : 3 = 3,1
х = 8,4 : 4
х = 2,1 — 1 число.
2) 2,1 + 0,9 = 3 — 2 число.
3) 2,1 · 2 = 4,2 — 3 число.
(Ответ: 2,1; 3; 4,2.)
IX. Повторение изученного материала
№ 582 стр. 95 (самостоятельно, устная проверка).
— Дополнительное задание: запишите числа, обратные данным.
(Ответ: 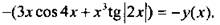 )
)
X. Самостоятельная работа
(На листочках записать промежуточные ответы, взаимопроверка на следующем уроке.)
Вариант I. № 581 стр. 95.
Вариант II. № 621 стр. 101.
XI. Подведение итогов урока
— С пользой ли для вас прошел этот урок?
— Что нового узнали, какие умения и навыки приобрели?
— Что осталось непонятым?
(Выставление оценок.)
Домашнее задание
№ 591 (б), 592 (а—в), 593, 595 (а) стр. 96.