Цели: ввести правила умножения двух отрицательных чисел и чисел с разными знаками; развивать правильную математическую речь; формирование внутренних процессов интеллектуального, личностного, эмоционального развития.
Информация для учителя
При нахождении значений выражений учащиеся постоянно проговаривают правила сложения и вычитания, деления и умножения положительных и отрицательных чисел.
Ход урока
I. Организационный момент
«Математика — это больше, чем наука, это язык» (Н. Бор).
— В течение урока подумайте над этими словами.
II. Анализ контрольной работы
— Какое задание вам было трудно выполнить? Где было допущено больше всего ошибок?
(Учащиеся анализируют ошибки и фиксируют затруднения.) Повторить алгоритм понятий, способов действий, в которых допущена ошибка.
С помощью модели координатной прямой закрепить алгоритмы решением примеров.
III. Устный счет
1. Решите уравнения:
1) у : 13 = 5;
2) у – 13 = 5;
3) у + 13 = 5;
4) у · 13 = 5;
5) у – 13 = -5;
6) у + 13 = -5.
2. № 1136 стр. 194.
(Ответ: например, а = 5; b = 5: 5 — 5 = 5 — 5;
Равенство а — b = b — а верно при условии а = b.)
3. № 1137 стр. 194.
(Ответ: а — b > а + b при а > 0, b < 0.)
4. Из трех одинаковых по виду колец одно несколько легче других. Как найти его одним взвешиванием на чашечных весах?
5. Книга в переплете стоит 64 руб. Сколько стоит переплет книги, если известно, что сама книга дороже ее переплета на 60 руб.? (2 руб.)
IV. Индивидуальная работа
1 карточка
1. Решить уравнения: 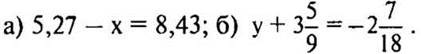
2. Найти расстояние между точками А (—3,5) и В (6,1).
3. Напиши все целые m, что 23 < | m | < 26.
2 карточка
1. Решить уравнения: 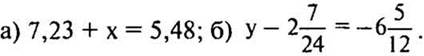
2. Найти расстояние между точками А (—7,5) и В (2,3).
3. Напиши все целые m, что 15 < | m | < 19.
V. Сообщение темы урока
— Сегодня на уроке мы узнаем, какие правила применяются при умножении положительных и отрицательных чисел.
VI. Изучение нового материала
1. Подготовительная работа.
— Где вы в жизни встречаетесь с отрицательными и положительными числами?
— Каким числом выражается увеличение величины, а каким — уменьшение? (Увеличение любой, величины можно выразить положительным числом, а уменьшение — отрицательным.)
2. Работа с учебником.
— Самостоятельно разберите задачи 1 и 2 в учебнике на стр. 190.
— Сформулируйте правило умножения чисел с разными знаками.
При умножении чисел с разными знаками:
1) перемножить модули этих чисел;
2) перед полученным числом поставить знак минус.
— Найдите значения выражений:
-0,5 · 7 = -3,5; 0,5 · (-7) = -3,5; 0,5 · 7 = 3,5.
— Сравните эти произведения с произведением 0,5 · 7 = 3,5.
— Какой вывод можно сделать? (При изменении знака любого множителя знак произведения меняется, а его модуль останется тем же.)
-0,5 · (-7) = 3,5.
— В данном произведении знаки меняются у обоих множителей, следовательно, и произведение дважды меняет знак. В результате знак произведения не меняется. Какой вывод можно сделать? (Произведение отрицательных чисел есть число положительное.)
— Сформулируйте правило умножения отрицательных дробей. Сравните свое правило с правилом в учебнике на стр. 191.
При умножении двух отрицательных чисел:
1) перемножить модули этих чисел;
2) перед полученным числом поставить знак плюс.
— При умножении отрицательных чисел принято первый множитель писать без скобок, так как (—1,5) · 3 = — (1,5 · 3) = 4,5.
— Найдите значения выражений:
-1,5 · (-3) = | -1,5 | · | -3 | = 1,5 · 3 = 4,5.
Можно писать короче:
-1,5 · (-3) = 1,5 · 3 = 4,5; -2,3 · (-2) = 4,6; -0,3 · (-7) = 2,1.
— Правила умножения можно истолковать и таким образом:
«Друг моего друга — мой друг»: + · + = +.
«Враг моего врага — мой друг»: — · — = +.
«Друг моего врага — мой враг»: + · — = +.
«Враг моего друга — мой враг»: — · + = — .
VII. Закрепление изученного материала
1. № 1118 стр. 191 (на доске и в тетрадях).
— Ответ обоснуйте.
Решение:
За (дм), при а = 4: 3 · 4 = 12 (дм) — уровень воды повысится. (Так как увеличение величины выражается положительным числом.);
при а = —3: 3 · (—3) = —9 (дм) — уровень воды понизится. (Так как уменьшение величины выражается отрицательным числом.)
2. № 1119 стр. 191 (устно).
Решение:
а) 3 · 15 = 45 (мм) — поднимется столбик ртути;
б) 3 · (—12) = —36 (мм) — опустится столбик ртути.
3. Прочитайте текст в учебнике на стр. 192 «Говори правильно».
VIII. Физкультминутка
IX. Работа над задачей
№ 1141 (а) стр. 194 (на обратной стороне доски и в тетрадях, самопроверка).
— Прочитайте задачу. Решите самостоятельно алгебраическим способом.
Решение:
1) Пусть х (м) — высота ели,
1,5х (м) — высота сосны.
Так как сосна выше ели на 1,2 м, то
1,5х – х = 1,2; 0,5х = 1,2; х = 12 : 5; х = 2,4
2,4 (м) — высота ели.
2) 2,4 + 1,2 = 3,6 (м) – высота сосны.
(Ответ: ель 2,4 м, сосна 3,6 м.)
X. Повторение изученного материала
Блиц-опрос.
— Сумма двух отрицательных чисел есть число… (отрицательное, положительное).
— Сумма двух противоположных чисел равна… (их сумме, нулю).
— При сложении двух чисел с разными знаками знак суммы совпадает со знаком того слагаемого, модуль которого… (больше, меньше).
— Чтобы из одного числа вычесть другое число, нужно… (к уменьшаемому прибавить; от уменьшаемого отнять) число, противоположное вычитаемому.
— Чтобы найти расстояние между двумя точками на координатной прямой, надо найти модуль… {разности, суммы) координат соответствующих точек.
XI. Самостоятельная работа (5—7 мин)
Вариант I
Выполните умножение: 10 · (-3,9); (-100) · 7,4; -65 · (-10); -2 · 2,4; 2 · (-2,9); (-5) · 1,2; -1,5 · (-3); -4 · 1,6.
Вариант II
Выполните умножение: 10 · (-6,3); (-10) · 3,1; -25 · (-100); -4 · 1,4; 2 · (-3,2); (-5) · 1,8; -1,7 · (-3); -6 · 1,2.
XII. Подведение итогов урока
— Сформулируйте правило умножения двух чисел с разными знаками.
— Как перемножаются два отрицательных числа?
Домашнее задание
Учебник, стр. 192 (прочитать текст под рубрикой «Говори правильно».) № 1143 (а—г), 1144 (а, б), 1145 (а, г), 1146 стр. 195.














