Цели: ознакомить с разложением на простые множители числа; повторить степень числа; формировать умения и навыки использования признаков делимости при разложении чисел на простые множители; развивать память.
Информация для учителя
При разложении натурального числа на простые множители учащиеся могут:
1) использовать таблицу простых чисел;
2) сначала найти два наиболее удобных множителя, затем их разложить на простые множители, записав решение в строчку;
3) брать в качестве делителей сразу простые числа (2, 3, 5, 7, 11 и т. д.), используя при этом признаки делимости на 2, на 3, на 5. Решение записать в столбик.
При разложении числа на простые множители в окончательном результате учащиеся должны записывать:
1) простые множители в порядке возрастания;
2) произведение одинаковых множителей представлять в виде степени.
Учащимся необходимо показать прием проверки правильности разложения числа на простые множители:
1) все числа из разложения должны быть простыми, свериться с таблицей простых чисел;
2) выполнить умножение простых чисел из разложения и проверить, получилось ли данное число.
Обратить внимание учеников на разный смысл выражений: «разложить натуральное число на множители», «разложить натуральное число на простые множители».
Ход урока
I. Организационный момент
II. Устный счет
1. № 103 (б, в) стр. 18. Записать ответы на листах. Фронтальная проверка.
— Кто не согласен с этим ответом?
2. Может ли простое число оканчиваться: а) цифрой 6; б) быть нечетным?
Ответ:
а) нет, так как это число является четным, значит, делится на 2;
б) да, так как все простые, кроме 2, являются нечетными.
3. Задание на развитие памяти. Посмотрите в течение 1 мин на числа.
17 77 31 144 32 555 41 23 54 888
Запишите их по памяти.
— Кто запомнил 8—10 чисел? Молодцы.
— 6-7 — неплохо.
— Кто запомнил меньше 6 чисел, потренируйте свою память.
— На какие группы можно разделить данные числа? Почему?
(1) простые и составные; 2) двухзначные и трехзначные; 3) четные и нечетные; 4) числа, для записи которых используют одинаковые цифры и разные цифры.)
— Назовите все простые числа от 2 до 20.
4. Запишите в виде степени произведение.
5. Назовите 2 числа, не равные нулю, сумма которых больше их произведения. (1 и 3, 1 и 8, 32 и 1.)
— Какой вывод можно сделать? (Сумма 1 и любого числа, отличного от нуля, всегда будет больше произведения этих чисел.)
6. Двое играли в шахматы 4 часа. Сколько времени играл каждый? (4 ч.)
III. Сообщение темы урока
— Мы с вами уже раскладывали числа на множители, но сегодня будет добавлено условие: на простые множители. В этом нам помогут знания признаков делимости чисел.
IV. Изучение нового материала
1. Подготовительная работа.
— Разложите на множители число 60 всеми возможными способами:
а) на 2 множителя; 60 = 2 · 30 = 3 · 20 = 4 · 15 = 5 · 12 = 6 · 10.
б) на 3 множителя; 60 = 2 · 5 · 6 = 2 · 3 · 10 = 2 · 2 · 15 = 3 · 4 · 5.
в) на 4 множителя; 60 = 2 · 2 · 3 · 5.
2. Работа над новой темой.
Эту тему учитель может разобрать вместе с учащимися по учебнику стр. 20 или рассказать сам.
а) — Разложите число 210 на 2 множителя, отличных от единицы. (210 = 21 · 10 = 14 · 15 = 7 · 30 = 70 · 3 = 6 · 35 = 42 · 5 = 105 · 2 — учащиеся могут предложить несколько вариантов ответов, учитель выбирает только один, на его примере дает объяснение нового материала).
210 = 21 · 10
— На какие два множителя можно разложить числа 21 и 10? (210 = 3 · 7 · 2 · 5.)
— Что можете сказать об этих множителях? (Являются простыми числами.)
— Таким образом, число 210 разложено на простые множители.
— Всякое составное число можно разложить на простые множители.
— Разложите самостоятельно число 120 на простые множителя любым способом.
(Записать на доске несколько вариантов ответов 120 = 3 · 2 · 5 · 2 · 2; 120 = 2 · 3 · 2 · 5 · 2.)
— Вы все раскладывали число 120 разными способами, но получили один и тот же результат. (120 = 2 · 2 · 2 · 3 · 5.)
— Какой вывод можно сделать? (При любом способе получается одно и то же разложение, если не учитывать порядка записи множителей.)
— Обычно записывают множители в порядке их возрастания, и произведение одинаковых множителей представляют в виде степени: 120 = 2 · 2 · 2 · 3 · 5 = 23 · 3 · 5.
б) Объяснение учителем разложения числа 756 на простые множители, аналогичное учебнику на стр. 21. (При этом повторяются признаки делимости чисел на 2, на 5, на 3.)
V. Физкультминутка
VI. Закрепление изученного материала
1. Разложите числа на простые множители (у доски и в тетрадях с подробным объяснением):
а) 20; б) 18; в) 32; г) 36; д) 13; е) 24; ж) 37; з) 45.
Ответ:
20 = 22 · 5; 18 = 2 · 32; 32 = 25; 36 = 22 · 32;
13?; 24 = 23 · 3; 37?; 45 = 32 · 5.
— Какие числа мы не разложили на простые множители? (13, 37.)
— Почему? (Простые числа не раскладываются.)
2. № 121 стр. 21. (а) — три числа). (У доски: 1 число — один ученик разбирает с подробным комментированием, потом работают сразу несколько ребят, остальные в тетрадях.)
VII. Рефлексия
У вас на столе фигуры.
— Я хорошо понял, как раскладывать числа на простые множители.
— Я не все понял, у меня были ошибки.
— Я не понял, как раскладывать числа на простые множители.
Учащимся предлагается выбрать символ и оценить свою деятельность. Дети сами вывешивают свои символы на магнитную доску.
VIII. Закрепление изученного материала
1. Индивидуальная работа.
К доске вызвать тех учащихся, которые не поняли, как раскладывать числа на простые множители. Учитель еще раз объясняет на примерах эту тему.
2. Самостоятельная работа.
Учащиеся выполняют самостоятельную работу.
Сверяют свои решения с ответами на закрывающейся доске.
— Разложите числа на простые множители.
Вариант I.80, 180, 108.
Вариант II. 60, 270, 72.
Вариант III (для слабых учащихся). 16, 40, 100.
(Ответы:
Вариант I. 80 = 24 · 5, 180 = 22 · 32 · 5, 108 = 22 · 33.
Вариант II. 60 = 22 · 3 · 5, 270 = 2 · 33 · 5, 72 = 23 · 32.
Вариант III. 16 = 24, 40 = 23 · 5, 100 = 22 · 52.)
3. № 124 (а, б, в), стр. 21. Аргументируйте свой ответ. Не забудьте найти, если можно, частное.
а) а делится на b без остатка, гак как в разложении числа а есть все множители числа b.
— Что нужно сделать, чтобы найти частное от деления а на b? (Нужно в произведении множителей числа а зачеркнуть множители числа b, оставшееся произведение множителей — искомое частное.)
4. Найдите все делители числа а:
а) а = 2 · 5 · 7;
б) 2 · 3 · 5 · 11.
— Что нужно сделать, чтобы найти делители? (Назвать все простые множители; затем их перемножить сначала парами, потом тройками и т. д.)
Решение:
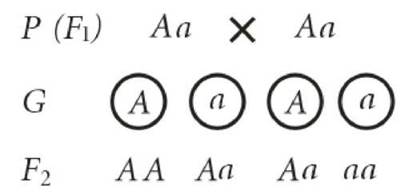
IX. Историческая минутка
Великий русский математик Пафнутий Львович Чебышев занимался изучением свойств простых чисел. Он доказал, что между любым натуральным числом, большим 1, и числом, вдвое большим, всегда имеется не менее одного простого числа. Проверить это можно на примере нескольких чисел.
X. Работа над задачей
№ 138 (1) стр. 23 (на доске и в тетрадях).
— Прочитайте задачу. О ком говорится в задаче?
— Что нам известно про первую бригаду?
— Что нам известно про вторую бригаду?
— Что значит на 1,52 ц больше?
— Назовите главный вопрос задачи.
— В краткой записи обведите его в кружок.
— Запишите краткую запись.
— Решим эту задачу алгебраическим способом, то есть с помощью уравнения.
— Что примем за x? (Сколько хлопка собрала 2-я бригада.)
— Тогда, что можно сказать о 1-й бригаде? (х + 1,52)
— На основании чего можно составить уравнение? (2 бригады вместе собрали 20,4 ц.)
Решение:
1) Пусть х (ц) – хлопка собрала 2-я бригада,
х + 1,52 (ц) — хлопка собрала 1-я бригада.
Зная, что 2 бригады вместе собрали 20,4 ц, составим уравнение:
х + х + 1,52 = 20,4
2х + 1,52 = 20,4
2х = 20,4 – 1,52
2х = 18,88
х= 18,88 : 2
х = 9,44; 9,44 (ц) — хлопка собрала 2-я бригада.
2) 9,44 + 1,52 = 10,96 (ц) — хлопка собрала 1-я бригада.
— Что надо сделать, чтобы записать ответ задачи? (Чтобы записать ответ задачи, надо прочитать вопрос задачи.)
— Запишите ответ задачи. (Если в последнем действии было пояснение, ответ можно записывать кратко.)
(Ответ: 9,44 ц, 10,96 ц.)
XI. Подведение итогов урока
— Что значит разложить число на простые множители? (Разложить натуральное число на простые множители — это значит представить это чиао в виде произведения простых чисел.)
— Единственно ли разложение натурального числа на простые множители? (Каким бы способом ни выполнялось разложение натурального числа на простые множители, мы получаем его единственное разложение, порядок множителей при этом не учитывается.)
Домашнее задание
№ 138 (2), 139 (1, 2), 141 (а) стр. 23. По желанию: проверьте утверждение П. Л. Чебышева.
