Цели: актуализировать знания учащихся об окружности и ее элементах; вывести формулы для нахождения длины окружности подлине ее диаметра и но длине ее радиуса; отрабатывать умение решать текстовые задачи на применение этих формул; формировать навык решения задач с помощью пропорций; развивать память и внимание.
Ход урока
I. Организационный момент
II. Актуализация опорных знаний учащихся
1. Познакомить учащихся с результатами самостоятельной работы.
2. Решить задания, где допущено наибольшее количество ошибок.
3. Работа над ошибками (в парах).
На листах формата А4 ребята в парах записывают решение, которое вывешивают на доске. Коллективное обсуждение.
III. Устный счет
1. Чему равен масштаб чертежа, если на нем детали увеличены в 20 раз?
Уменьшены в 5 раз?
2. Что больше:
23 или 32; 52 или 5 · 5; 42 или 4 · 2; 62 или 6 + 6?
3. Задание на развитие памяти.
— Посмотрите 10 сек. на доску.
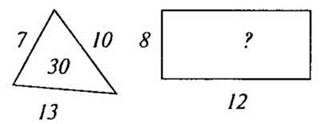
1 рисунок
— Что изображено на 1 рисунке?
— Какое число находится внутри треугольника?
— Какие числа на сторонах треугольника?
— Найдите закономерность расположения чисел.
2 рисунок
— Что изображено на 2 рисунке?
— Где находится число 8?
— Где находится число 15? (Такого числа не было.)
— Какое число было и где?
— Какое число нужно вставить вместо знака вопроса? (40.)
— Почему? (Сумма длин сторон прямоугольника.)
— Как называется сумма длин сторон прямоугольника? (Периметр.)
IV. Сообщение темы урока
— Сегодня мы узнаем, как находить длину окружности и площадь круга.
V. Изучение нового материала
1. Актуализация опорных знаний.
— Ответьте на вопросы:
1. Что называют отношением двух величин?
2. Как округлить десятичную дробь до десятых? До сотых?
3. Чему равна площадь прямоугольника?
4. Если фигуру площадью S разделить на части с площадями S1 и S2, будет ли выполняться равенство S = S1+ S2?
5. Если фигуру площадью S разделить на части и из них составить другую фигуру, будет ли ее площадь равна площади первоначальной фигуры?
2. Практическая работа.
а) Мне нужны два помощника.
— Возьмем круглый предмет и обведем его мелом на доске, а вы у себя в тетради обведите модели кругов. На доске и у вас в тетрадях получится окружность.
— Что такое окружность? (Замкнутая линия. Все точки окружности одинаково удалены от ее центра.)
— Возьмем нитку, обмотаем ее вокруг нашего стакана (цилиндра, подставки для карандашей, ручки), а потом распрямим нить.
— Длина нити будет приближенно равна длине нарисованной окружности.
— Проверим. Обмотайте нить по нарисованной в тетради окружности. Попросите помощи у товарища.
— Измерьте, чему равна длина вашей окружности.
— Как это сделать? (Измерить длину нити.)
б) Начертите с помощью циркуля окружность.
— Центр окружности обозначим точкой О.
— Дайте определение окружности. (Все точки находятся на одинаковом расстоянии от центра окружности.)
— Выберите любую точку на окружности. Обозначим ее А.
— Как называется отрезок ОА? (Радиус.)
— Постройте еще одну окружность.
— Проведите отрезок, проходящий через центр окружности.
— Как он называется? (Диаметр.)
— Чему равен диаметр? (Он в 2 раза больше радиуса.)
— Диаметр в переводе с греческого слова означает «поперечник». У древнегреческих математиков слово употреблялось и в значении «диагональ».
— С помощью нити измерьте длину окружности.
— Измерьте длину диаметра.
(Записать на доске несколько вариантов измерений.)
3. Работа над новой темой.
— Какой вывод можно сделать? (Длина окружности прямо пропорциональна длине ее диаметра.)
— Найдите отношение длины окружности к длине ее диаметра. (Можно воспользоваться микрокалькулятором.)
— Какое число у вас получилось? (Бесконечная десятичная дробь.)
(Записать на доске ответы детей.)
— Округлите ее до тысячных, до сотых, до десятых, до единиц.
— Что интересного заметили? (Хотя окружности были построены у всех разные, отношения длины окружности к диаметру получились примерно одинаковые.)
— Какой вывод можно сделать? (Отношение длины окружности к длине ее диаметра является одним тем же числом.)
По ходу объяснения записывать на доске и в тетрадь.
— Это число обозначают греческой буквой ж.
— Подсчеты показали, что с точностью до десятитысячных π ≈ 3,1416.
— Запоминание величины π (3,1416) связывают с предложением «Что я знаю о круге», где количество букв в каждом слове равно соответствующей цифре числа п.
— Округлите это значение до сотых: 3,1416.
— Читают: «Пи приближенно равно трем целым четырнадцати сотым».
— Примерно такую же точность дает значение π ≈ 22/7.
— В старших классах вы узнаете, как проводились такие расчеты. Число 22/7 носит имя великого математика: называется оно «число Архимеда».
— Обозначим длину окружности буквой С, а длину диаметра буквой d.
— Вспомним, как мы находили π. π = С · d.
— Выразим из этой формулы С: С = πd.
— Так как d = 2r, то по-другому можно записать формулу длины окружности: С = 2πr.
Записи в тетради:
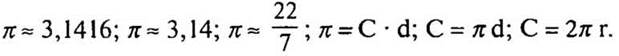
VI. Физкультминутка
VII. Закрепление изученного материала
(При решении задач можно просить, чтобы учащиеся всегда записывали формулы, по которым они решают. Можно постоянно проговаривать эти формулы. Оформлять задачи учитель может по своему усмотрению.)
1. № 847 стр. 139 (у доски и в тетрадях).
(Слабым детям можно разрешить найти значение выражения с помощью микрокалькулятора.)
— Прочитайте задачу.
— Что известно? Что надо узнать?
— Как узнать длину окружности, зная ее радиус?
— Запишем решение.
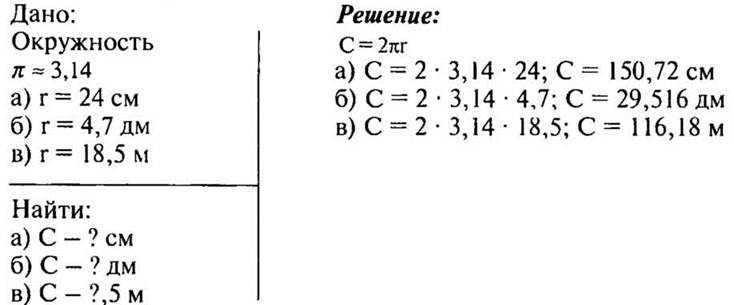
(Ответы: а) С = 150,72 см; б) С = 29,516 дм; в) С = 116,18 м.)
2. № 849 стр. 139 (один ученик решает у доски, остальные — в тетрадях).
— Прочитайте задачу.
— Что известно? Что надо узнать?
— Как найти длину окружности, зная ее диаметр?
— Запишем решение.

Найти:
С — ? см
(Ответ: С = 155 см.)
VIII. Самостоятельная работа
Вариант 1
№ 851 (первое значение) стр. 139, № 829 стр. 135.
Вариант II
№ 851 (второе значение) стр. 139, № 858 стр. 140.