Цель: рассмотреть способы решения тригонометрических неравенств.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
Решите уравнение:
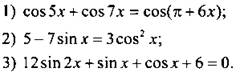
Вариант 2
Решите уравнение:
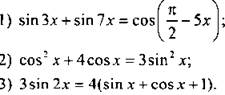
III. Изучение нового материала
Решение тригонометрических неравенств (как и уравнений), как правило, сводится к решению простейших тригонометрических неравенств. Поэтому прежде всего остановимся на решении таких неравенств. Их удобно решать, используя единичную окружность.
Пример 1
Решим неравенство sin x > 1/2.
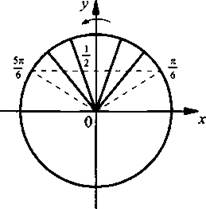
На единичной окружности по оси ординат отложим значение sin х = 1/2 и построим соответствующие углы ![]() (углы откладываются против часовой стрелки и являются положительными). На рисунке видно, что неравенству sin х > 1/2 удовлетворяют значения
(углы откладываются против часовой стрелки и являются положительными). На рисунке видно, что неравенству sin х > 1/2 удовлетворяют значения ![]() Учтем, что период функции синуса составляет 2π, и получим решение данного неравенства
Учтем, что период функции синуса составляет 2π, и получим решение данного неравенства ![]() или
или ![]()
Пример 2
Решим неравенство ![]()
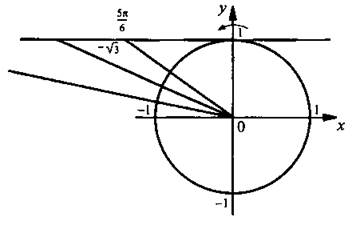
На оси котангенсов для единичной окружности отложим значение ![]() и построим соответствующий угол
и построим соответствующий угол ![]() Видно, что неравенству
Видно, что неравенству ![]() удовлетворяют значения
удовлетворяют значения ![]() Учитывая период функции котангенса (равный π), получим решение данного неравенства:
Учитывая период функции котангенса (равный π), получим решение данного неравенства: ![]() или
или ![]() где n ∈ Z.
где n ∈ Z.
В случае сложного аргумента тригонометрической функции рекомендуется обозначить его новой переменной, решить для него неравенство, а затем вернуться к старой неизвестной.
Пример 3
Решим неравенство ![]()
Обозначим аргумент косинуса ![]() и получим простейшее тригонометрическое неравенство
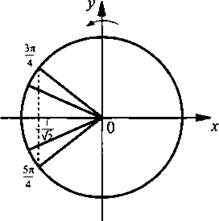
и получим простейшее тригонометрическое неравенство ![]() Решим это неравенство. На единичной окружности по оси абсцисс отложим значение
Решим это неравенство. На единичной окружности по оси абсцисс отложим значение ![]() и построим соответствующие углы
и построим соответствующие углы ![]() Тогда неравенству
Тогда неравенству ![]() удовлетворяют значения
удовлетворяют значения ![]() Учтем периодичность функции cos y и получим решения
Учтем периодичность функции cos y и получим решения ![]()
Теперь вернемся к старой неизвестной х и получим двойное линейное неравенство ![]() Ко всем частям неравенства прибавим число π/6. Отсюда
Ко всем частям неравенства прибавим число π/6. Отсюда ![]() Все части неравенства разделим на положительное число 3. При этом знак неравенства сохраняется. Получим:
Все части неравенства разделим на положительное число 3. При этом знак неравенства сохраняется. Получим: ![]() или
или ![]() где n ∈ Z.
где n ∈ Z.
Если неравенство не является простейшим, то используя преобразования, аналогичные тем, которые применялись для уравнений, сводим неравенство к простейшему.
Пример 4
Решим неравенство ![]()
Введем новую переменную у = tg x и получим квадратное неравенство ![]() Это неравенство имеет решение
Это неравенство имеет решение ![]() Вернемся к старой неизвестной x и получим двойное неравенство
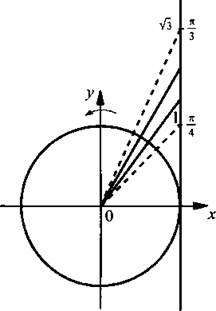
Вернемся к старой неизвестной x и получим двойное неравенство ![]() На единичной окружности по оси тангенсов отложим значения 1 и
На единичной окружности по оси тангенсов отложим значения 1 и ![]() и построим соответствующие углы
и построим соответствующие углы ![]() Тригонометрическому неравенству удовлетворяют значения
Тригонометрическому неравенству удовлетворяют значения ![]() Учтем периодичность функции тангенса и получим решение данного неравенства:
Учтем периодичность функции тангенса и получим решение данного неравенства: ![]() или
или 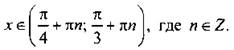
Также при решении тригонометрических неравенств можно использовать метод интервалов (который является универсальным для всех неравенств).
Пример 5
Решим неравенство 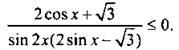
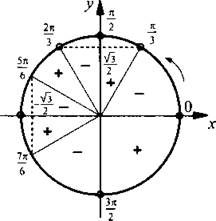
На единичной окружности отметим значения х, при которых обращается в нуль числитель ![]() (откуда
(откуда ![]() ) и знаменатель sin 2х = 0 (тогда
) и знаменатель sin 2х = 0 (тогда ![]() )
) ![]() (откуда
(откуда ![]() ) дроби. Определим знак этой дроби, например, при х = π/6 и получим:
) дроби. Определим знак этой дроби, например, при х = π/6 и получим:
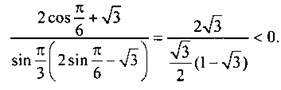
Учтем, что при переходе через отмеченные значения х знак неравенства меняется на противоположный. Построим диаграмму знаков данной дроби. Также учтем значения х, при которых знаменатель дроби обращается в нуль (они отмечены кружками). Теперь легко выписать решения неравенства: ![]() Учитывая, что через 2пn (где n ∈ Z) ситуация повторяется, выпишем решения данного неравенства:
Учитывая, что через 2пn (где n ∈ Z) ситуация повторяется, выпишем решения данного неравенства: ![]()
![]()
При наличии в неравенстве функций тангенса и котангенса удобно перейти к функциям синуса и косинуса и использовать рассмотренный метод интервалов.
Пример 6
Решим неравенство ![]()
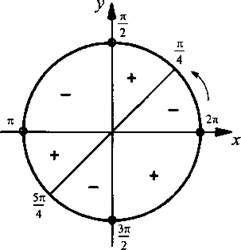
Учтем, что ![]() и запишем неравенство в виде
и запишем неравенство в виде ![]() Отметим на единичной окружности значения х, при которых обращается в нуль числитель sin x – cos x= 0 (откуда
Отметим на единичной окружности значения х, при которых обращается в нуль числитель sin x – cos x= 0 (откуда ![]() и
и ![]() ) и знаменатель sin x cos x = 0 (тогда
) и знаменатель sin x cos x = 0 (тогда ![]() и x = 2π) дроби. Определим знак данной дроби, например, при х = π/3 и получим:
и x = 2π) дроби. Определим знак данной дроби, например, при х = π/3 и получим:
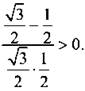
Учтем, что при переходе через отмеченные значения x знак неравенства меняется на противоположный. Построим диаграмму знаков данной дроби. Учтем также значения х, при которых знаменатель дроби обращается в нуль (они отмечены кружками). С учетом периодичности функций синуса и косинуса, входящих в неравенство, запишем окончательное решение данного неравенства ![]() где n ∈ Z
где n ∈ Z














