Цели: дать понятие предела функции; рассмотреть простейшие его свойства.
Ход уроков
I. Сообщение темы и целей уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Найдите сумму геометрической прогрессии 9, 3, 1, 1/3, ….
2. Решите уравнение 2х + 4х2 + 8х3 +… = 3 (где |х| < 1).
3. Представьте в виде обыкновенной дроби 0,(16).
Вариант 2
1. Найдите сумму геометрической прогрессии 8, 3, 1/2, 1/8, ….
2. Решите уравнение 3х + 6х2 + 12х3 + …-2 (где |х| < 1).
3. Представьте в виде обыкновенной дроби 0,(24).
III. Изучение нового материала
Понятие и строгое определение предела функции достаточно сложные, и многие студенты их не воспринимают и не умеют ими пользоваться. Поэтому на этом занятии мы попытаемся дать некие представления о пределе функции и его свойствах, не вводя строгого определения предела. Все-таки при этом попытаемся связать предел функции с пределом последовательности (что обсуждалось ранее).
1. Предел функции на бесконечности
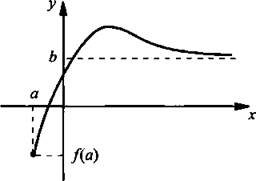
Будем рассматривать поведение функции у = f(х) при х → +∞. Пусть область определения такой функции D(f) = [а; +∞). Возьмем последовательность аргументов хn = а + n (где n ∈ N ) и соответствующую ей последовательность значений уn = f(xn) функции в этих точках. Пусть предел такой последовательности ![]() Разумно считать, что число b является и пределом функции у = f(х) при стремлении x к плюс бесконечности. Для описания этой математической модели используют запись
Разумно считать, что число b является и пределом функции у = f(х) при стремлении x к плюс бесконечности. Для описания этой математической модели используют запись ![]() При этом прямая у = b является горизонтальной асимптотой графика функции у = f(х). Другими словами, при х → +∞ значения функции у = f(х) практически равны числу b.
При этом прямая у = b является горизонтальной асимптотой графика функции у = f(х). Другими словами, при х → +∞ значения функции у = f(х) практически равны числу b.
Пример 1
Найдем предел функции ![]()
Рассмотрим последовательность аргументов хn = n (где n ∈ N).
Очевидно, что при n → ∞ аргументы хn → +∞. Соответствующая последовательность значений функции имеет вид: ![]() Предел такой последовательности легко вычисляется:
Предел такой последовательности легко вычисляется: 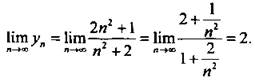 Тогда и предел данной функции
Тогда и предел данной функции ![]()
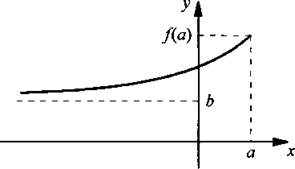
Аналогично можно дать определение предела функции у = f(x) при х → -∞. Пусть область определения этой функции D(f) = (-∞; а]. Рассмотрим последовательность аргументов хn = а – n (где n ∈ N), которая при n → ∞ стремится к -∞ (т. е. хn → -∞). Возьмем соответствующую ей последовательность значений уn = f(хn) функции в этих точках. Пусть предел такой последовательности ![]() Тогда будем считать, что число b является и пределом функции у = f(х) при стремлении х к минус бесконечности, т. е.
Тогда будем считать, что число b является и пределом функции у = f(х) при стремлении х к минус бесконечности, т. е. ![]() При этом прямая у = b будет горизонтальной асимптотой графика функции у = f(x).
При этом прямая у = b будет горизонтальной асимптотой графика функции у = f(x).
Если выполнены соотношения ![]() то их объединяют одной записью
то их объединяют одной записью ![]() или еще более короткой записью
или еще более короткой записью ![]() (читают: предел функции у = f(х) при стремлении х к бесконечности равен b).
(читают: предел функции у = f(х) при стремлении х к бесконечности равен b).
Так как предел функции связан с пределом последовательности, то при вычислении подобных пределов используются аналогичные теоремы.
1) Для любого натурального показателя т справедливо соотношение ![]()
2) Если ![]() то:
то:
а) предел суммы равен сумме пределов, т. е. ![]()
![]()
б) предел произведения равен произведению пределов, т. е. ![]()
в) предел частного равен частному пределов (при с ≠ 0), т. е. 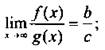
г) постоянный множитель можно вынести за знак предела, т. е. ![]()
В силу этих теорем вычисление пределов функции похоже на вычисление пределов последовательностей.
Пример 2
Найдем ![]()
Преобразуем данную функцию ![]() Для этого выражение умножим и разделим на сопряженную величину:
Для этого выражение умножим и разделим на сопряженную величину: 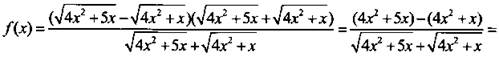
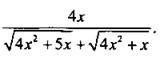 Теперь легко вычислить предел функции:
Теперь легко вычислить предел функции: 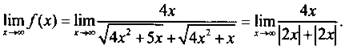 Отсюда
Отсюда ![]() и
и ![]()
2. Предел функции в точке
Такое понятие характеризует поведение функции у = f(х) в окрестности точки х = а. При этом в самой точке х = а функция может и не существовать. Попробуем сформулировать понятие предела функции у = f(x) в точке х = а. Рассмотрим последовательности аргументов ![]() которые сходятся к точке а, т. е. хn → а при n → ∞. Также рассмотрим соответствующие последовательности уn = f(хn) значений функции. Пусть
которые сходятся к точке а, т. е. хn → а при n → ∞. Также рассмотрим соответствующие последовательности уn = f(хn) значений функции. Пусть ![]() Тогда разумно считать, что число b является пределом функции у = f(x) в точке х = а. При этом используют запись
Тогда разумно считать, что число b является пределом функции у = f(x) в точке х = а. При этом используют запись ![]() (читают: предел функции у = f(x) при стремлении х к а равен b).
(читают: предел функции у = f(x) при стремлении х к а равен b).
Обсудим три часто встречающиеся ситуации (см. рисунок).
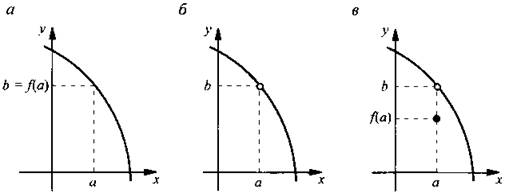
За исключением точки х = а, функции одинаковы, пределы этих функций ![]() также равны. Отличие функций состоит в следующем: в случае а функция существует во всех точках и предел функции равен ее значению в точке а (т. е. b = f(a)); в случае б функция не определена в точке а (т. е. f(a) не существует); в случае в функция определена во всех точках, но b ≠ f(a).
также равны. Отличие функций состоит в следующем: в случае а функция существует во всех точках и предел функции равен ее значению в точке а (т. е. b = f(a)); в случае б функция не определена в точке а (т. е. f(a) не существует); в случае в функция определена во всех точках, но b ≠ f(a).
Таким образом, графический смысл предела заключается в следующем: если значения аргумента выбирать все ближе и ближе к значению х = а, то соответствующие значения функции все меньше и меньше будут отличаться от предела b.
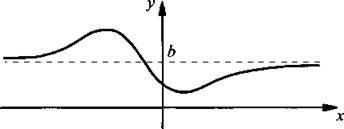
Заметим, что положение еще сложнее. Обсудим функцию, график которой приведен на рисунке.
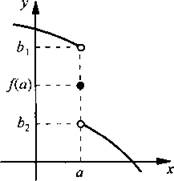
Функция у = f(x) определена во всех точках. Что касается предела функции, то ситуация усложняется. Видно, что при стремлении х к а слева (т. е. при х < a) ![]() при стремлении х к а справа (т. е. при х > a)
при стремлении х к а справа (т. е. при х > a) ![]() Поэтому начинает возникать понятие одностороннего предела функции. Сейчас мы не имеем возможности углубляться в эти понятия. Однако помните, что функции и их графики могут быть очень непривычными и сложными. Чтобы их характеризовать, и приходится вводить все более и более сложные понятия.
Поэтому начинает возникать понятие одностороннего предела функции. Сейчас мы не имеем возможности углубляться в эти понятия. Однако помните, что функции и их графики могут быть очень непривычными и сложными. Чтобы их характеризовать, и приходится вводить все более и более сложные понятия.
Обсудим теперь очередное понятие – непрерывность функции y = f(x) в точке х = а. Ранее мы говорили, что функция непрерывна, если ее график представляет собой сплошную линию (без разрывов, выколотых точек и т. д.). Таковой является функция а на рис. а-в.
Определение 1. Функцию у = f(x) называют непрерывной в точке х = а, если предел функции при стремлении хка равен ее значению в этой точке, т. е. ![]()
Пример 3
Докажем, что функция у = х2 непрерывна в любой точке х = а.
Сначала найдем предел функции ![]() Рассмотрим последовательность
Рассмотрим последовательность ![]() (где n ∈ N), сходящуюся к а. Тогда
(где n ∈ N), сходящуюся к а. Тогда 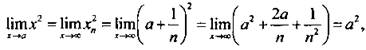 так как
так как ![]() и
и ![]() С другой стороны, f(a) = а2. Видно, что
С другой стороны, f(a) = а2. Видно, что ![]()
![]() Поэтому по определению данная функция у = x2 непрерывна в любой точке х = а.
Поэтому по определению данная функция у = x2 непрерывна в любой точке х = а.
Функция у = f(x) непрерывна на промежутке X, если она непрерывна в каждой точке этого промежутка.
В курсе математического анализа доказано утверждение: если выражение f(x) составлено из рациональных, иррациональных, тригонометрических выражений, то функция у = f(x) непрерывна в любой точке, в которой определено выражение f(x).
Понятие непрерывности функции помогает вычислять пределы функции, так как ![]()
Пример 4
Найдем ![]()
Данная функция ![]() определена в точке х = 1. Поэтому
определена в точке х = 1. Поэтому ![]()
Пример 5
Вычислим 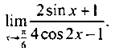
Функция ![]() определена в точке х = π/6. Получим:
определена в точке х = π/6. Получим: 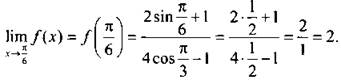
Если функция у = f(х) не определена в точке х = а, то предел функции также можно вычислить.
Пример 6
Найдем ![]()
При x = 4 числитель и знаменатель функции ![]() равны нулю, а делить на нуль нельзя. Поэтому сократим дробь:
равны нулю, а делить на нуль нельзя. Поэтому сократим дробь: ![]() Теперь вычислим предел этой функции:
Теперь вычислим предел этой функции: ![]() Заметим, что выражения
Заметим, что выражения ![]() совпадают при х ≠ 4. Причем для вычисления предела функции при x → 4 саму точку x = 4 исключают из рассмотрения.
совпадают при х ≠ 4. Причем для вычисления предела функции при x → 4 саму точку x = 4 исключают из рассмотрения.
Пример 7
Вычислим ![]()
1-й способ. Поступим аналогично предыдущему примеру и сократим дробь. Для этого числитель и знаменатель умножим на величину ![]() Получим:
Получим: 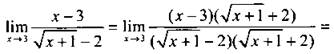
![]()
2-й способ. Введем новую переменную ![]() Тогда при х → 3 величина
Тогда при х → 3 величина ![]() и х = z<
и х = z<














