Цель: рассмотреть основные свойства функций.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Постройте график функции:
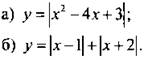
2. Постройте график неравенства 
Вариант 2
1. Постройте график функции:
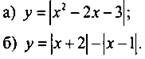
2. Постройте график неравенства 
III. Изучение нового материала
Четко сформулируем основные свойства функций, на которые необходимо обращать внимание при исследовании функций и построении их графиков.
1. Точки пересечения графика функции с осями координат
Остановимся теперь на основных свойствах функции. С двумя свойствами функции вы уже знакомы – это область определения и область изменения функции. Рассмотрим следующее свойство функции – точки пересечения графика функции с осями координат.
Так как ось 0y характерна тем, что любая точка на ней имеет координату х = 0, а для оси 0х – любая точка на ней имеет координату у = 0, то точки пересечения графика с осями координат ищут очень просто. Точка пересечения с осью 0y равна значению функции f(х) при х = 0, т. е. f(0). Точки пересечения с осью 0х являются корнями уравнения f(x) = 0.
Пример 1
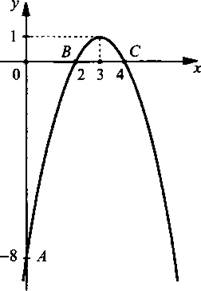
Рассмотрим функцию у(x) = -х2 + 6х – 8. Найдем точки пересечения графика этой функции с осями координат. Чтобы определить точку пересечения графика с осью ординат, вычислим значение функции y(x) при х = 0: у(0) = -02 + 6 · 0 – 8 = -8. Получим координаты этой точки А(0; -8).
Теперь определим точки пересечения графика данной функции с осью абсцисс. Для этого в функцию у = -х2 + 6х – 8 подставим значение у = 0 и получим квадратное уравнение 0 = -х2 + 6х – 8 или 0 = х2 – 6х + 8.
Решим его: 
Поэтому график функции пересекает ось абсцисс в двух точках – В(2; 0) и С(4; 0). Для наглядности на рисунке приведен график данной функции.
2. Монотонность функции
Рассмотрим еще одно свойство функции – монотонность (т. е. возрастание или убывание функции).
Определение 1. Функция называется возрастающей, если большему значению аргумента соответствует большее значение функции (т. е. если х2 > х1, то f(х2) > f(х1)).
Определение 2. Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции (т. е. если х2 > х1, то f(x2) < f(х1)). На рисунках приведены графики монотонных (возрастающей и убывающей) и немонотонной функций.
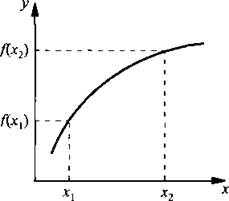
Возрастающая функция, f(x2) > f(х1)
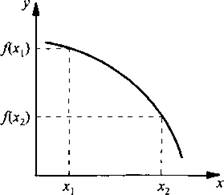
Убывающая функция, f(x2) < f(х1)
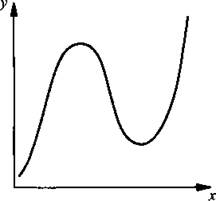
Немонотонная функция
Пример 2
Определим монотонность функции f(х) = -2х + 4.
Область определения этой функции – все значения х, т. е. х ∈ (-∞; +∞). Возьмем два значения х из области определения этой функции – x1 и х2, и пусть х2> x1. Найдем значения функции в этих точках: f(x1) = -2х1 + 4 и f(x2) = -2х2 + 4. Теперь необходимо сравнить эти значения и определить, какое из них больше. Для этого рассмотрим разницу этих величин f(х2) – f(x1) = (-2х2 + 4) – (-2х1 + 4) = -2х2 + 4 + 2х1 – 4 = -2(х2 – x1).
Так как х2 > x1, то разность х2 – x1 > 0 и величина -2(х2 – x1) < 0. Поэтому получим:f(х2) – f(x1) < 0 или f(х2) < f(x1). Это неравенство означает, что большему значению аргумента соответствует меньшее значение функции. Поэтому данная функция (по определению) является убывающей. Это же видно из приведенного графика функции.
Функция на всей области определения может быть немонотонной, но на отдельных промежутках может быть монотонной. Например, функция f(х) = -х2 + 6х – 8 в целом немонотонна, но на промежутке х ∈ [3; +∞) функция убывает, а на промежутке х ∈ (-∞; 3] – возрастает (докажем это). Соответственно, такие промежутки называют промежутками убывания и возрастания функции f(x).
Пример 3
Областью определения функции f(х) = -х2 + 6х – 8 является D(f) = (-∞; ∞). Возьмем два значения х из области определения: x1 и х2, и пусть х2 > x1. Найдем значения функции в этих точках: 
и 
Сравним эти значения. Рассмотрим разность этих величин: 
Первый множитель х2 – х1 в этом произведении положительный, так как х2 > x1 по договоренности. Второй же множитель может иметь разный знак. Рассмотрим два случая.
а) Пусть x1 < х2 ≤ 3, тогда x1 + х2 < 6 и второй множитель 6 – x1 – х2 > 0. Поэтому произведение положительно и f(х2) – f(х1) > 0, т. е. f(х2) > f(х1). Следовательно, функция f(х) возрастает на промежутке (-∞; 3];
б) пусть х2 > х1 ≥ 3, тогда x1 + х2 > 6 и второй множитель 6 – x1 – х2 < 0. Поэтому произведение отрицательно f(x2) – f(х1) < 0, т. е. f(х2) < f(х1). Следовательно, функцияf(х) убывает на промежутке [3; ∞).
Из графика данной функции видны промежутки возрастания и убывания.
Если область определения функции состоит из нескольких промежутков, то при исследовании функции на монотонность надо выбирать точки x1 и х2, лежащие в одном промежутке.
Пример 4
Исследуем на монотонность функцию f(x) = 1/x.
Область определения данной функции – промежутки (-∞; 0) и (0; ∞). График этой функции (гипербола) хорошо известен.
Видно, что функция убывает в области определения. Исследуем ее на монотонность. Выберем точки х1 и х2 из области определения так, что х2 > x1. Найдем разность 
Так как х2 > x1, то числитель этой дроби отрицательный. Если x1 и х2 лежат в одном промежутке области определения (т. е. x1, х2 < 0 или x1, х2 > 0), то произведение x1 · х2 > 0. Поэтому дробь отрицательна, т. е. f(х2) – f(x1) < 0 илиf(х2) < f(x1). В итоге получаем правильный результат – функция является убывающей.
Если x1 и х2 лежат в разных промежутках области определения (т. е. x1 < 0 и х2 > 0), то произведение x1 · х2 < 0. Поэтому дробь положительна, т. е. f(х2) – f(x1) > 0 или f(х2) > f(x1). В результате получаем грубую ошибку – функция является возрастающей.
3. Ограниченность функций
Определение 3. Функцию f(х) называют ограниченной снизу, если все значения этой функции больше некоторого числа m, т. е. f(х) > m. График функции целиком лежит выше прямой y = m.
Определение 4. Функцию f(х) называют ограниченной сверху, если все значения этой функции меньше некоторого числа М, т. е. f(х) < М. График функции целиком лежит ниже прямой у = М.
На рисунках приведены графики функций – ограниченной снизу (а), ограниченной сверху (б) и неограниченной (в). Если функция ограничена и снизу, и сверху на всей области определения, то ее называют ограниченной.
f(х) > m. Ограничена снизу
f(х) < М. Ограничена сверху
Не ограничена
Пример 5
Выясним ограниченность функции у = -х2 + 6x – 8.
В данной функции выделим полный квадрат у = -(х2 – 6х + 8) = -((х – 3)2 -1) = 1 – (х – 3)2. Так как (x – 3)2 ≥ 0, то при всех значениях х значения у(х) ≤ 1. В качестве числа М можно взять любое из чисел 2, 
, π и т. д. Тогда у(х) < M и данная функция по определению ограничена сверху. Это же видно из рисунка примера 1.
Заметим, что более перспективным является другой способ решения. Предположим, что данная функция ограничена, т. е. при всех значениях х выполнено неравенство m < у(х) < М или m < -х2 + 6х – 8 < М. Найдем такие числа m и М.
Запишем данное двойное неравенство в виде системы квадратных неравенств 
или 
Рассмотрим две вспомогательные функции: y1 =x2 – 6x + 8 + m и у2 = х2 – 6х + 8 + М. Их графиками являются параболы, направленные ветвями вверх. Очевидно, что неравенство у1 < 0 при всех х выполняться не может. Неравенство у2 > 0 будет выполняться при всех значениях х, если дискриминант квадратного трехчлена 
откуда М > 1. Таким образом, данная функция ограничена сверху и не ограничена снизу.
Рассмотрим более сложный пример на использование такого способа решения.
Пример 6
Выясним ограниченность функции 
Предположим, что данная функция ограничена, т. е. существуют такие числа m и М, что выполнено неравенство m < у(х) < М и 
при всех значениях х.
Так как при всех значениях х выражение х2 + х + 1 > 0, то умножим все части двойного неравенства на это выражение: 
Запишем такое неравенство в виде системы неравенств 
или 
Рассмотрим две вспомогательные функции: 
Чтобы выполнялись неравенства у1 > 0 и у2 > 0 при всех х, надо, чтобы выполнялись условия:
1) парабола направлена ветвями вверх, т. е. старший коэффициент квадратного трехчлена положительный;
2) дискриминант квадратного трехчлена отрицательный.
Получим систему неравенств 
или 
или 
откуда m < 1/3. Поэтому данная функция ограничена снизу. В качестве m можно взять, например, число 1/10.
Аналогично получим еще одну систему неравенств 
или 
или 
откуда М > 3. Таким образом, данная функция ограничена и сверху. В качестве М можно взять, например, число π = 3,14.
Следовательно, функция y(x) ограничена и снизу, и сверху, т. е. ограничена.
4. Экстремумы функции
При исследовании поведения функции вблизи некоторой точки х = а удобно пользоваться понятием окрестности этой точки. Окрестностью точки а называют любой интервал, содержащий эту точку. Например, интервалы (3; 10), (4; 6), (4,8; 5,1) – некот
