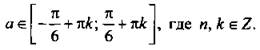Цель: проверить знания учащихся по вариантам одинаковой сложности.
Ход уроков
I. Сообщение темы и цели уроков
II. Характеристика зачетной работы
III. Варианты зачетной работы
Вариант 1
А
1. Дано: ![]() Найдите sin a, tg a, ctg a.
Найдите sin a, tg a, ctg a.
2. Сравните числа cos14°cos74° и ½.
3. Вычислите ![]()
4. Постройте график функции ![]()
5. Решите уравнение ![]()
6. Решите неравенство ![]()
7. Упростите выражение ![]()
В
8. Дано: ![]() Найдите cos a – sin a.
Найдите cos a – sin a.
9. Сравните числа ![]()
10. Найдите область значений функции ![]()
11. Упростите выражение ![]()
12. Найдите значение выражения 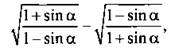 если
если ![]()
13. Найдите множество значений функции ![]()
14. Решите уравнение ![]()
Вариант 2
А
1. Дано: ![]() Найдите sin a, tg a, ctg a.
Найдите sin a, tg a, ctg a.
2. Сравните числа 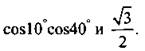
3. Вычислите 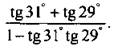
4. Постройте график функции ![]()
5. Решите уравнение ![]()
6. Решите неравенство ![]()
7. Упростите выражение ![]()
В
8. Дано: 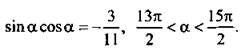 Найдите cos а – sin а.
Найдите cos а – sin а.
9. Сравните числа ![]()
10. Найдите область значений функции у = 12 sin x + 5 cos x – 4.
11. Упростите выражение 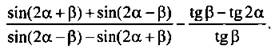
C
12. Найдите значение выражения 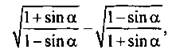 если
если ![]()
13. Найдите множество значений функции 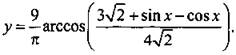
14. Решите уравнение ![]()
IV. Ответы и решения
Вариант 1
![]()
2. Второе число больше.
![]()
4. График у = 2|cos х|.
9. Первое число больше.
10. Е(у) = [-10; 16].
11. -1.
12. В подкоренных выражениях умножим числители и знаменатели дробей на сопряженную величину знаменателя. Получим
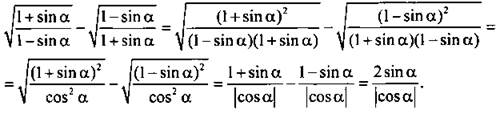
В силу ограниченности функции sin а при всех а величины ![]() Так как
Так как ![]() то cos a < 0 и |cos a| = -cos a. Поэтому выражение
то cos a < 0 и |cos a| = -cos a. Поэтому выражение ![]() Для значения tg a = -1/3 найдем значение данного выражения:
Для значения tg a = -1/3 найдем значение данного выражения: ![]()
Ответ: 2/3.
13. Используем метод введения вспомогательного угла и преобразуем функцию: ![]()
![]() Учтем, что функция арксинуса возрастающая, и запишем неравенства
Учтем, что функция арксинуса возрастающая, и запишем неравенства ![]()
![]() тогда -6 ≤ y ≤ 2. Таким образом, множество значений данной функции Е(у) = [-6; 2].
тогда -6 ≤ y ≤ 2. Таким образом, множество значений данной функции Е(у) = [-6; 2].
Ответ: [-6; 2].
14. Преобразуем сумму двух последних функций в произведение: sin x + 2 sin a cos х = 2. Используем метод введения вспомогательного угла. Разделим все члены уравнения на ![]() Получаем:
Получаем: 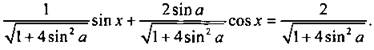 Будем считать, что
Будем считать, что ![]() тогда tgφ = 2 sin a и φ = arctg(2 sin a). Уравнение имеет вид:
тогда tgφ = 2 sin a и φ = arctg(2 sin a). Уравнение имеет вид: ![]() решения которого
решения которого ![]() и
и 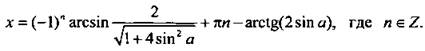 При этом должно выполняться неравенство
При этом должно выполняться неравенство ![]() Решим его и получим:
Решим его и получим: ![]() или
или ![]() илиcos 2a ≤ -1/2, откуда
илиcos 2a ≤ -1/2, откуда 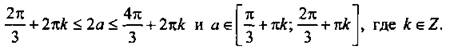
Ответ: ![]() при
при 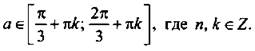
Вариант 2
![]()
2. Второе число больше.
![]()
4. График у = 2|sin2x|.
![]()
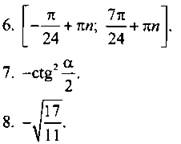
9. Второе число больше.
10. Е(у) = [-9; 17].
11. 1.
12. В подкоренных выражениях умножим числители и знаменатели дробей на сопряженную величину знаменателя. Получим:
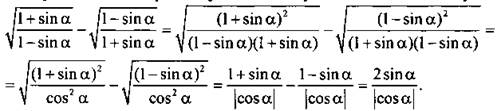
В силу ограниченности функции sin а при всех а величины ![]() Так как
Так как ![]() то cos a > 0 и |cos a| = cos a. Поэтому выражение
то cos a > 0 и |cos a| = cos a. Поэтому выражение ![]() Для значения tg a = -1/2 найдем значение данного выражения: 2 · (-1/2) = -1.
Для значения tg a = -1/2 найдем значение данного выражения: 2 · (-1/2) = -1.
Ответ: -1.
13. Используем метод введения вспомогательного угла и преобразуем функцию: ![]()
![]() Учтем, что функция арккосинуса убывающая, и запишем неравенства
Учтем, что функция арккосинуса убывающая, и запишем неравенства ![]()
![]() тогда 3 ≥ у ≥ 0. Таким образом, множество значений данной функции Е(у) = [0; 3].
тогда 3 ≥ у ≥ 0. Таким образом, множество значений данной функции Е(у) = [0; 3].
Ответ: [0; 3].
14. Преобразуем сумму двух последних функций в произведение: sin х + 2 cos a cos x= 2. Используем метод введения вспомогательного угла. Разделим все члены уравнения на ![]() Получим:
Получим: ![]() Будем считать, что
Будем считать, что ![]() тогда tg φ = 2 cos a и φ = arctg(2 cos a). Уравнение имеет вид:
тогда tg φ = 2 cos a и φ = arctg(2 cos a). Уравнение имеет вид: 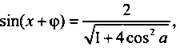 решения которого
решения которого 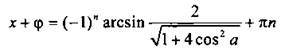 и
и 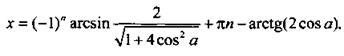 При этом должно выполняться неравенство
При этом должно выполняться неравенство ![]() Решим его и получим:
Решим его и получим: ![]() или
или ![]() или
или ![]() откуда
откуда 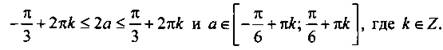
Ответ: ![]() при
при