Цель: закончить изучение основных тригонометрических формул.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Напишите формулы для:
![]()
2. Упростите выражение ![]()
3. Решите уравнение ![]()
Вариант 2
1. Напишите формулы для:
![]()
2. Упростите выражение ![]()
3. Решите уравнение ![]()
III. Изучение нового материала
Чтобы закончить изучение этой темы, необходимо рассмотреть последнюю группу формул – преобразования произведений тригонометрических функций в суммы:
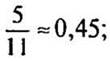
Пример 1
Выведем формулу (16).
Используя соотношение (5), запишем: ![]()
![]() Вычтем из первого выражения второе и получим:
Вычтем из первого выражения второе и получим: ![]() откуда
откуда ![]()
Пример 2
Вычислим ![]() Используя формулы (16)—(18), запишем:
Используя формулы (16)—(18), запишем: ![]()
![]() Здесь учтено, что cos 90° = 0. Рассмотрим
Здесь учтено, что cos 90° = 0. Рассмотрим ![]()
![]() и
и ![]() Получим:
Получим: ![]()
Пример 3
Найдем наименьшее и наибольшее значения выражения ![]() Используя формулу (18), получим:
Используя формулу (18), получим: 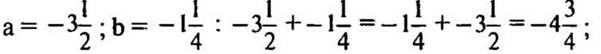
![]() Оценим эту величину:
Оценим эту величину: ![]() тогда
тогда ![]() (все части неравенства умножили на положительное число 1/2) и
(все части неравенства умножили на положительное число 1/2) и ![]() (ко всем частям прибавили 1/4). Итак, получили:
(ко всем частям прибавили 1/4). Итак, получили: ![]() т. е. наименьшее значение Анаим = -1/4 и наибольшее значение Анаи6 = 3/4.
т. е. наименьшее значение Анаим = -1/4 и наибольшее значение Анаи6 = 3/4.
Пример 4
Решим уравнение ![]()
Используя формулу (17), получим: ![]()
![]() или cos 11x =cos 23x. Запишем уравнение в виде cos 11x – cos 23x = 0 и представим разность косинусов в виде произведения функций: 2 sin 17x sin 6х = 0. Получим совокупность уравнений sin 17х = 0 (тогда
или cos 11x =cos 23x. Запишем уравнение в виде cos 11x – cos 23x = 0 и представим разность косинусов в виде произведения функций: 2 sin 17x sin 6х = 0. Получим совокупность уравнений sin 17х = 0 (тогда ![]() ) и sin 6х = 0 (тогда
) и sin 6х = 0 (тогда ![]() ).
).
IV. Контрольный вопрос
Формулы преобразования произведений тригонометрических функций в суммы.
V. Задание на уроках
§ 23, № 1 (а, б); 2 (в, г); 3 (а, б); 4 (а); 5 (б); 6 (а); 7 (б); 8 (а); 9 (б); 10 (а, б); 11 (а); 12 (6); 13.
VI. Задание на дом
§ 23, № 1 (в, г); 2 (а, б); 3 (в, г); 4 (б); 5 (а); 6 (б); 7 (а); 8 (б); 9 (а); 10 (в, г); 11 (б); 12 (a).
VII. Подведение итогов уроков














