Цель: проверить знания учащихся по вариантам одинаковой сложности.
Ход уроков
I. Сообщение темы и цели уроков
II. Характеристика зачетной работы
III. Варианты зачетной работы
Вариант 1
А
1. Вычислите ![]()
2. Решите неравенство 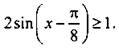
3. Найдите решения уравнения 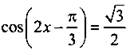 на промежутке [0; 2π].
на промежутке [0; 2π].
4. Найдите область определения и область значений функции у = arcsin|x|.
5. Решите уравнение:
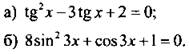
6. Постройте график функции у = arccos х + arccos(-x).
В
7. Решите уравнение ![]()
8. Найдите область определения и область значений функции ![]()
9. Решите уравнение ![]()
10. Решите неравенство ![]()
С
11. Решите уравнение:
![]()
![]()
12. Постройте график функции 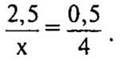
Вариант 2
А
1. Вычислите 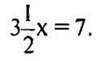
2. Решите неравенство ![]()
3. Найдите решения уравнения 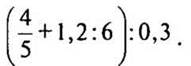 на промежутке [0; 2π].
на промежутке [0; 2π].
4. Найдите область определения и область значений функции у = arccos|x|.
5. Решите уравнение:
![]()
6. Постройте график функции у = arcctg x + arcctg(-x).
В
7. Решите уравнение ![]()
8. Найдите область определения и область значений функции ![]()
9. Решите уравнение ![]()
10. Решите неравенство 2 cos2 x + cos х ≤ 0.
С
11. Решите уравнение:
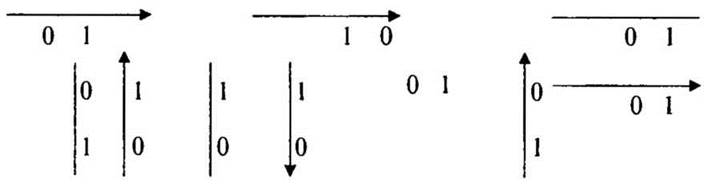
12. Постройте график функции 
IV. Ответы и решения
Вариант 1
![]()
11, а. Используем равенство sin2 x + cos2 х = 1 и приведем уравнение к однородному тригонометрическому уравнению второй степени ![]() или
или ![]()
![]() Разделим все члены уравнения на cos2 x и получим: tg2x + 5tg х + 4 = 0. Введем новую переменную z = tg x и придем к квадратному уравнениюz2 + 5z + 4 = 0, корни которого z1 = -1 и z2 = -4. Вернемся к старой неизвестной и получим простейшие тригонометрические уравнения tg x = -1 (решения
Разделим все члены уравнения на cos2 x и получим: tg2x + 5tg х + 4 = 0. Введем новую переменную z = tg x и придем к квадратному уравнениюz2 + 5z + 4 = 0, корни которого z1 = -1 и z2 = -4. Вернемся к старой неизвестной и получим простейшие тригонометрические уравнения tg x = -1 (решения ![]() ) и tg х = -4 (решения
) и tg х = -4 (решения ![]() ).
).
Ответ: ![]()
11, б. Запишем данное уравнение в виде ![]()
![]() Учтем, что sinх ≤ 0, и возведем обе части уравнения в квадрат:
Учтем, что sinх ≤ 0, и возведем обе части уравнения в квадрат: ![]() или
или ![]() Введем новую переменную z = cos х и получим квадратное уравнение
Введем новую переменную z = cos х и получим квадратное уравнение![]() корни которого
корни которого ![]() (не подходит, так как z ≤ 1) и
(не подходит, так как z ≤ 1) и ![]() Вернемся к старой неизвестной и получим систему
Вернемся к старой неизвестной и получим систему  Решения этой системы
Решения этой системы ![]()
Ответ: ![]()
12. Построим сначала аргумент  данной функции у(х).
данной функции у(х).
Функция z(x) четная, и ее график симметричен относительно оси ординат. При x = 0 значение ![]() при х → ∞ значения z → 1 (а). Учтем, что
при х → ∞ значения z → 1 (а). Учтем, что ![]() После этого легко построить график данной функции
После этого легко построить график данной функции 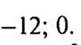 (б).
(б).
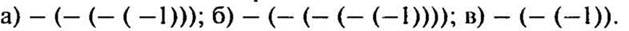
Ответ: график построен.
Вариант 2
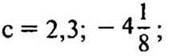
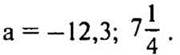
11, а. Используем равенство sin2 x + cos2 = 1 и приведем уравнение к однородному тригонометрическому уравнению второй степени ![]() или
или ![]()
![]() Разделим все члены уравнения на cos2 x и получим: tg2x – 3tg х + 2 = 0. Введем новую переменную z = tg х и придем к квадратному уравнениюz2 – 3z + 2 = 0, корни которого z1 = 1 и z2 = 2. Вернемся к старой неизвестной и получим простейшие тригонометрические уравнения tg х = 1 (решения
Разделим все члены уравнения на cos2 x и получим: tg2x – 3tg х + 2 = 0. Введем новую переменную z = tg х и придем к квадратному уравнениюz2 – 3z + 2 = 0, корни которого z1 = 1 и z2 = 2. Вернемся к старой неизвестной и получим простейшие тригонометрические уравнения tg х = 1 (решения ![]() ) и tg x = 2 (решения
) и tg x = 2 (решения ![]() ).
).
Ответ: ![]()
11, б. Для уравнения ![]() очевидно, что cos х ≥ 0. Возведем обе части уравнения в квадрат:
очевидно, что cos х ≥ 0. Возведем обе части уравнения в квадрат: ![]()
![]() Запишем его в виде
Запишем его в виде ![]()
![]() или
или ![]() Введем новую переменную z =sin х и получим квадратное уравнение
Введем новую переменную z =sin х и получим квадратное уравнение ![]() корни которого
корни которого ![]() (не подходит, так как z ≤ 1) и
(не подходит, так как z ≤ 1) и ![]() Вернемся к старой переменной и получим систему
Вернемся к старой переменной и получим систему 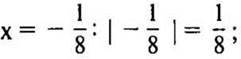 Решения этой системы
Решения этой системы ![]()
Ответ: ![]()
12. Построим сначала аргумент ![]() данной функции у(х). Функция z(x) четная, и ее график симметричен относительно оси ординат. При х = 0 значение
данной функции у(х). Функция z(x) четная, и ее график симметричен относительно оси ординат. При х = 0 значение ![]() при х → ∞ значения z → 1 (a). Учтем, что
при х → ∞ значения z → 1 (a). Учтем, что ![]() и
и ![]() После этого легко построить график данной функции
После этого легко построить график данной функции 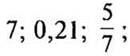 (б).
(б).
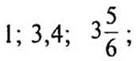
Ответ: график построен.