Цель: рассмотреть решение тригонометрических уравнений.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Дайте определение и перечислите основные свойства функции у = arctg х.
2. Постройте график функции:
3. Вычислите 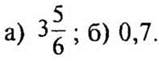
Вариант 2
1. Дайте определение и перечислите основные свойства функции у = arcctg х.
2. Постройте график функции:
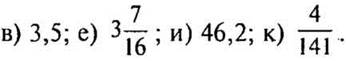
3. Вычислите ![]()
III. Изучение нового материала
Рассмотрим решение некоторых типов тригонометрических уравнений. Для этого необходимо с помощью преобразований данное уравнение свести к одному из простейших уравнений – sin x = a, cos х = a, tg х = a, ctg х = a, решение которых можно записать.
1. Простейшие тригонометрические уравнения
Еще раз напомним решения простейших тригонометрических уравнений.
1. Решения уравнений sin x = а (где |a| ≤ 1) имеют вид: ![]()
2. Решения уравнений cos x = а (где |а| ≤ 1) имеют вид: ![]()
3. Решения уравнений tg x = а имеют вид: ![]()
4. Решения уравнений ctg x = а имеют вид: ![]()
При решении уравнений sin x = 0; ±1 и cos x = 0; ±1 (частные случаи) удобнее пользоваться не общими формулами, а использовать числовую окружность, тогда получим:
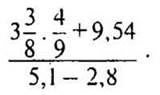
Пример 1
Для уравнения sin x = 1 покажем предпочтительность использования числовой окружности.
Сначала запишем решения уравнения sin x = 1, применяя общую формулу ![]() Для нескольких значений n такие решения приведены в таблице.
Для нескольких значений n такие решения приведены в таблице.
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
|
x |
|
|
|
|
|
|
Из данных таблицы видно, что при использовании формулы ![]() каждое решение повторяется по два раза. Кроме того, выражение
каждое решение повторяется по два раза. Кроме того, выражение ![]() более громоздко по сравнению с формулой
более громоздко по сравнению с формулой ![]() которая получается при рассмотрении числовой окружности.
которая получается при рассмотрении числовой окружности.
Пример 2
Найдем решения уравнения ![]() принадлежащие отрезку [0; π].
принадлежащие отрезку [0; π].
Решим данное уравнение, используя числовую окружность. Получим: ![]() Отберем те решения, которые принадлежат отрезку [0; π]. По условию получим неравенство
Отберем те решения, которые принадлежат отрезку [0; π]. По условию получим неравенство ![]() Решим это неравенство:
Решим это неравенство: ![]() В этот промежуток попадают три целых значения n: n = 0, 1, 2. Для этих значении n найдем соответствующие решения:
В этот промежуток попадают три целых значения n: n = 0, 1, 2. Для этих значении n найдем соответствующие решения: ![]()
![]()
Пример 3
Решим уравнение ![]()
Используя общую формулу, получим: ![]()
![]() Тогда
Тогда ![]()
2. Два основных метода решения тригонометрических уравнений
Для решения более сложных уравнений используют метод введения новой переменной и метод разложения на множители. Рассмотрим сначала метод введения новой переменной.
Пример 4
Решим уравнение: ![]()
а) Введем новую переменную z = cos x и получим квадратное уравнение ![]() корни которого z1 = 1 и z2 = 2/3. Вернемся к старой неизвестной и получим простейшие уравнения cos x = 1 и cos x = 2/3. Решения первого уравнения x = 2πn, решения второго уравнения
корни которого z1 = 1 и z2 = 2/3. Вернемся к старой неизвестной и получим простейшие уравнения cos x = 1 и cos x = 2/3. Решения первого уравнения x = 2πn, решения второго уравнения ![]()
б) Используя формулу ![]() в уравнении перейдем к функции sin x. Получим:
в уравнении перейдем к функции sin x. Получим: ![]() или
или ![]() Далее поступаем аналогично пункту а. Введем новую переменную z = sin x и получим квадратное уравнение
Далее поступаем аналогично пункту а. Введем новую переменную z = sin x и получим квадратное уравнение ![]() корни которого z1 = 2 и z2 = 1/3. Вернемся к старой неизвестной и получим простейшие уравнения sin х = 2 (решений не имеет) и sin х = 1/3 (его решения
корни которого z1 = 2 и z2 = 1/3. Вернемся к старой неизвестной и получим простейшие уравнения sin х = 2 (решений не имеет) и sin х = 1/3 (его решения ![]() ).
).
Теперь обсудим второй метод – метод разложения на множители. При его применении уравнение f(x) = 0 записывают в виде ![]() , тогда или f1(x) = 0, или f2(х) = 0. Таким образом, задача сводится к решению совокупности уравнений
, тогда или f1(x) = 0, или f2(х) = 0. Таким образом, задача сводится к решению совокупности уравнений ![]()
Пример 5
Решим уравнение: ![]()
а) Левая часть уравнения уже разложена на множители. Задача сводится к решению совокупности уравнений tg х – 1 = 0 (или tg x = 1) и cos x + 1/2 = 0 (или cos x = -1/2). Решения первого уравнения ![]() решения второго уравнения
решения второго уравнения ![]()
б) Вынесем cos 3x за скобки и получим: ![]() Теперь необходимо решить совокупность уравнений cos 3x = 0 и
Теперь необходимо решить совокупность уравнений cos 3x = 0 и ![]() (или
(или ![]() ). Решая первое уравнение, найдем:
). Решая первое уравнение, найдем: ![]() и
и ![]() Решая второе уравнение, получим:
Решая второе уравнение, получим: ![]()
Уточним рассматриваемый метод. Из уравнения ![]() следует, что или f1(x) = 0 (при этом выражение f2(х) имеет смысл), или f2(х) = 0 (при этом выражение f1(х) имеет смысл).
следует, что или f1(x) = 0 (при этом выражение f2(х) имеет смысл), или f2(х) = 0 (при этом выражение f1(х) имеет смысл).
Пример 6
Решим уравнение ctg x(cos + 1) = 0.
Из уравнения ctg x = 0 находим: ![]() из уравнения cos х + 1 = 0 (илиcos х = -1) получим: x = π + 2πn. Но при таких значениях х выражение ctg x не имеет смысла. Поэтому решения данного уравнения х = π/2 + пn.
из уравнения cos х + 1 = 0 (илиcos х = -1) получим: x = π + 2πn. Но при таких значениях х выражение ctg x не имеет смысла. Поэтому решения данного уравнения х = π/2 + пn.
3. Однородные тригонометрические уравнения
Теперь обсудим часто встречающийся вид уравнений – однородные уравнения.
Определение. Уравнение вида ![]() (где а ≠ 0, b ≠ 0) называют однородным тригонометрическим уравнением первой степени. Уравнение вида
(где а ≠ 0, b ≠ 0) называют однородным тригонометрическим уравнением первой степени. Уравнение вида ![]() (где а ≠ 0) называют однородным тригонометрическим уравнением второй степени.
(где а ≠ 0) называют однородным тригонометрическим уравнением второй степени.
Рассмотрим сначала решение однородных тригонометрических уравнений первой степени ![]() Убедимся, что cos х ≠ 0. Предположим, что cos х = 0, и подставим эту величину в данное уравнение. Получим: a sin х = 0. Так как а ≠ 0, то sin x= 0. Очевидно, что равенства cos x = 0 и sin x = 0 одновременно выполняться не могут, так как равенство sin2x + cos2x = 1 не выполняется.
Убедимся, что cos х ≠ 0. Предположим, что cos х = 0, и подставим эту величину в данное уравнение. Получим: a sin х = 0. Так как а ≠ 0, то sin x= 0. Очевидно, что равенства cos x = 0 и sin x = 0 одновременно выполняться не могут, так как равенство sin2x + cos2x = 1 не выполняется.
Так как cos x ≠ 0, то разделим все члены уравнения на cos x. Получим: ![]() или
или ![]() откуда
откуда ![]() и
и ![]()
Пример 7
Решим уравнение 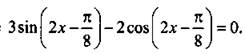
Разделим все члены уравнения на ![]() и получим:
и получим: ![]() Найдем
Найдем ![]() и
и ![]()
Пример 8
Решим уравнение ![]()
Учтем четность функции косинуса и формулы приведения. Получим: ![]() или
или ![]() Разделим обе части уравнения на cos 3x. Имеем: 2tg 3x = -1, откуда tg 3x = -1/2,
Разделим обе части уравнения на cos 3x. Имеем: 2tg 3x = -1, откуда tg 3x = -1/2, ![]()
Рассмотрим теперь решение однородного тригонометрического уравнения второй степени ![]() Убедимся, что cos х ≠ 0. Подставим значениеcos х = 0 в данное уравнение и получим: a sin2 х = 0. Так как а ≠ 0, то имеем: sin х = 0. Но равенства cos х = 0 и sin х = 0 одновременно выполняться не могут.
Убедимся, что cos х ≠ 0. Подставим значениеcos х = 0 в данное уравнение и получим: a sin2 х = 0. Так как а ≠ 0, то имеем: sin х = 0. Но равенства cos х = 0 и sin х = 0 одновременно выполняться не могут.
Так как cos x ≠ 0, то разделим все члены уравнения на cos2x и получим: ![]() или
или ![]() Введем новую переменную z = tg xи придем к квадратному уравнению az2 + bz + c = 0. Решаем это уравнение. Потом возвращаемся к старой переменной, получаем простейшие тригонометрические уравнения и находим их решения.
Введем новую переменную z = tg xи придем к квадратному уравнению az2 + bz + c = 0. Решаем это уравнение. Потом возвращаемся к старой переменной, получаем простейшие тригонометрические уравнения и находим их решения.
Пример 9
Решим уравнение ![]()
Разделим все члены уравнения на cos2 x и получим: tg2 x – tg x – 2 = 0. Введем новую переменную z = tg x и получим квадратное уравнение z2 – z – 2 = 0, корни которого z1 = -1 и z2 = 2. Вернемся к старой переменной. Имеем простейшие тригонометрические уравнения tg х = -1 (его решения ![]() ) и tg х = 2 (его решения
) и tg х = 2 (его решения ![]() ).
).
Пример 10
Решим уравнение ![]()
Данное уравнение не является однородным, так как в правой части стоит число 1, а не число 0. Если учесть равенство sin2 х +cos2 х = 1, то уравнение легко свести к однородному. Получим: ![]()
![]() или
или ![]()
![]() Разделим все члены уравнения на cos2 x. Имеем: tg2 x + 5tg x + 4 = 0. Введем новую переменную z = tg x и получим квадратное уравнение z2 + 5z + 4 = 0, корни которого z1 = -1 и z2 = -4. Вернемся к старой переменной. Получим простейшие тригонометрические уравнения tg x = -1 (его решения
Разделим все члены уравнения на cos2 x. Имеем: tg2 x + 5tg x + 4 = 0. Введем новую переменную z = tg x и получим квадратное уравнение z2 + 5z + 4 = 0, корни которого z1 = -1 и z2 = -4. Вернемся к старой переменной. Получим простейшие тригонометрические уравнения tg x = -1 (его решения ![]() ) и tg х = -4 (его решения
) и tg х = -4 (его решения ![]() ).
).
Пусть в однородном тригонометрическом уравнении ![]() коэффициент a = 0. Тогда уравнение имеет вид:
коэффициент a = 0. Тогда уравнение имеет вид: ![]() В этом случае делить на cos2 x нельзя, так как cos х может равняться нулю. Поэтому надо использовать метод разложения на множители. Получим
В этом случае делить на cos2 x нельзя, так как cos х может равняться нулю. Поэтому надо использовать метод разложения на множители. Получим ![]() Имеем простейшее тригонометрическое уравнение cos x = 0 и однородное тригонометрическое уравнение первой степени
Имеем простейшее тригонометрическое уравнение cos x = 0 и однородное тригонометрическое уравнение первой степени ![]() Такие уравнения мы решать уже умеем.
Такие уравнения мы решать уже умеем.
Пример 11
Решим уравнение ![]()
Разложим левую часть уравнения на множители: ![]() Произведение двух множителей равно нулю. Поэтому один из множителей равен нулю. Получаем простейшее тригонометрическое уравнение cos х = 0 (его решения
Произведение двух множителей равно нулю. Поэтому один из множителей равен нулю. Получаем простейшее тригонометрическое уравнение cos х = 0 (его решения ![]() ) и однородное тригонометрическое уравнение первого порядка
) и однородное тригонометрическое уравнение первого порядка ![]() или
или ![]() (его решения
(его решения ![]() ).
).
Метод разложения на множители также используется и в случае, когда коэффициент с = 0. Тогда уравнение имеет вид: ![]() или
или ![]() Вновь получаем простейшее тригонометрическое уравнение sin х = 0 и однородное тригонометрическое уравнение первого порядка
Вновь получаем простейшее тригонометрическое уравнение sin х = 0 и однородное тригонометрическое уравнение первого порядка ![]() которые решаются аналогично примеру 11.
которые решаются аналогично примеру 11.
Рассмотрение примеров 9-11 позволяет сформулировать алгоритм решения уравнения ![]()
1. Если коэффициент а не равен нулю, то все члены уравнения делят на cos2 x. Вводят новую переменную z = tg х и получают квадратное уравнение. Находят корни этого уравнения и возвращаются к старой неизвестной. Получают простейшие тригонометрические уравнения и решают их.
2. Если коэффициенты а и с равны нулю, то используют метод разложения на множители. При a = 0 выносят за скобки cos х, при с = 0 выносят sin x. Получают простейшее тригонометрическое уравнение и однородное тригонометрическое уравнение первого порядка и решают их.
IV. Контрольные вопросы
1. Решения простейших тригонометрических уравнений.
2. Два основных метода решения тригонометрических уравнений.
3. Определение однородного тригонометрического уравнения первой и второй степеней.
4. Решение однородного тригонометрического уравнения первой степени.
5. Алгоритм решения однородного тригонометрического уравнения второй степени.
V. Задание на уроках
§ 18, № 3 (а, в); 5 (а, б); 6 (б); 8 (г); 10 (а, б); 11 (в); 12 (а); 13 (в); 16; 18; 20 (а); 21 (а, б); 23 (а); 27 (а, б); 30 (а); 31; 33 (а); 34 (б); 35 (а).
VI. Задание на дом
§ 18, № 3 (б, г); 5 (в, г); 6 (г); 8 (б); 10 (в, г); 11 (а); 12 (б); 13 (г); 17; 19; 20 (б); 21 (в, г); 23 (б); 27 (в, г); 30 (б); 32; 33 (б); 34 (а); 35 (б).
VII. Подведение итогов уроков