Цели: сообщить результаты работы; рассмотреть типичные ошибки; разобрать трудные задачи.
Ход урока
I. Сообщение темы и целей урока
II. Итоги контрольной работы
III. Ответы и решения
Вариант 1
1. х = arctg 1,5 + πn (где n ∈ Z).
2. Промежутки возрастания (-∞; -5] и [1; ∞), промежуток убывания [-5; 1], хmах = -5 и 
xmin = 1 и 
3. Доказано.
4. yнаиб = f(-1) = 15, yнаим = f(3) = -17.
5. min f(х) = f(0) = -5, точки пересечения с осью абсцисс х = ±1.
6. 40, 80, 60.
Вариант 2
1. х = -arctg 2/3 + πn (где n ∈ Z).
2. Промежутки возрастания (-∞; -4] и [1; ∞), промежуток убывания [-4; 1], хmах = -4 и 
xmin = 1 и 
3. Доказано.
4. yнаиб = f(1) = 8, унаим = f(-2) = -73.
5. min f(х) = f(0) = -9, точки пересечения с осью абсцисс х = ±1.
6. 80, 120,100.
Вариант 3
1. 5π/6 + 2πn (где n ∈ Z).
2. Промежуток возрастания [2; ∞), промежутки убывания 
3. Учесть возрастание функции.
4. yнаиб = f(-2) = 32, унаим = f(-5) = -49.
5. 
6. a = 2.
Вариант 4
1. π/3 + 2пn (где n ∈ Z).
2. Промежуток возрастания 
экстремумов нет.
3. Учесть возрастание функции.
4. унаиб = f(0) = 32, унаим = f(4) = 0.
5. 
6. a = 6.
Вариант 5
1. Найдем наибольшее значение данной функции. Сначала вычислим производную функции 
Стационарные точки функции на заданном промежутке задаются условиями sin x = 0 иcos 2x = -1/3. Для первого случая (sin x = 0 или х = 0; ±π) имеем: f(х) = 0. Для второго случая ( cos 2x = -1/3) получим: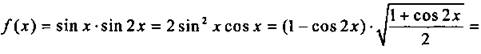 
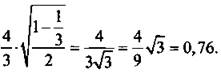
Ответ: доказано.
2, а. График функции пересекает ось абсцисс в точке 
и ось ординат – в точке у = 4, имеет вертикальную асимптоту х = 1 и горизонтальную асимптоту у = 1. Найдем производную функции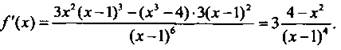 
Стационарные точки функции x = ±2. При этом хmin = -2 и ymin = f(-2) = 4/9; хmax = 2 и ymах = f(2) = 4. Исследовав промежутки возрастания и убывания функции, легко построить график функции.
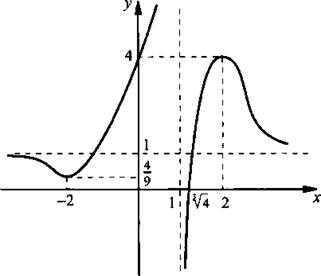
Ответ: см. график.
2, б. После построения графика функции f(х) легко ответить на вопрос о количестве корней уравнения f(x) = а. Имеем при 
1 корень; при 
2 корня; при 
3 корня.
Ответ: при 1 корень; при 2 корня; при 
3 корня.
3. ОДЗ данного уравнения х = 27/2. Производная левой части уравнения f1′(х) = 3х2 – 6х + 9 при всех х положительна. Производная правой части уравнения 
отрицательна при х ∈ (-∞; 13,5). Тогда по теореме о корне данное уравнение имеет единственный корень, который находится подбором. Получаем х = 1. Ответ: х = 1.
4. Пусть одно из чисел равно х, тогда второе равно 20 – х. Найдем сумму куба первого числа и квадрата второго числа и получим функцию f(х) = х3 + (20 – х)2. Найдем ее производную: 
Стационарные точки функции 
или x1 = -4 и х2 = 10/3. Отметим эти точки на координатной оси и нарисуем диаграмму знаков производной. Видно, что функция имеет минимум при х = 10/3. Тогда второе число 20 – х = 50/3. Эти два числа положительные, что соответствует условию задачи.
Заметим, что если числа поменять местами, то по аналогии будем иметь функцию f(х) = (20 – х)3 + х2. Производная этой функции 
Видно, что функция f(x) убывает при всех х и наименьшего значения не имеет.
Ответ: 10/3 и 50/3.
5. Легко сообразить, что с > 0. Пусть касание происходит в точке а. Найдем f’(х) = 2сх и напишем уравнение касательной: у = 2са(х – а) + са2 или у = 2сах – са2.
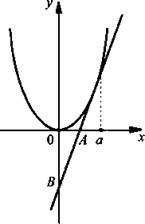
Найдем координаты точек пересечения касательной с осями координат. При х = 0 имеем: у = -са2 и ОВ = са2. При у = 0 получаем уравнение 0 = 2сах – са2, откуда х = a/2 и ОА = a/2. Тогда 
Учтем, что 
и запишем условия задачи: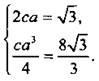 
Из этой системы уравнений надо найти с. Возведем в куб первое уравнение 
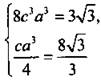и разделим первое уравнение на второе: с2 = 9/256 и с = 3/16 (учтено, что с > 0). Кстати, легко найти и точку касания: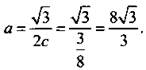 
Ответ: с = 3/16.
Вариант 6
1. Найдем наименьшее значение данной функции. Сначала вычислим производную функции: 
Стационарные точки функции на заданном промежутке задаются условиями cos х = 0 иcos 2х = 1/3. Для первого случая (cos х = 0 или х = ±π/2) имеем: f(х) = 0. Для второго случая (cos 2x = 1/3) получим: 
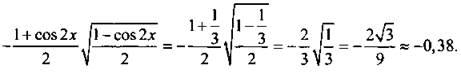Так как -0,38 > -7/18, то yнаим< -7/18.
Ответ: доказано.
2, а. График функции пересекает ось абсцисс в точке 
и ось ординат – в точке у = 4. Имеет вертикальную асимптоту х = -1 и горизонтальную асимптоту у = 1. Найдем производную функции: 
Стационарные точки функции х = ±2. При этом xmin = 2 и ymin = f(2) = 4/9; xmax = -2 и ymax = f(-2) = 4. Исследовав промежутки возрастания и убывания, легко построить график функции.
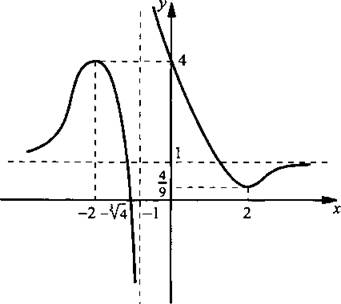
Ответ: см. график.
2, б. После построения графика функции f(х) легко ответить на вопрос о количестве корней уравнения f(х) = а. Имеем при 
1 корень; при 
2 корня; при 
3 корня.
Ответ: при 
1 корень; при 2 корня; при 
3 корня.
3. ОДЗ данного уравнения х ≤ 19/2. Производная левой части уравнения f1’(x) = 3х2 – 4х + 8 при всех х положительна. Производная правой части уравнения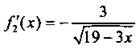 
отрицательна при 
Тогда по теореме о корне данное уравнение имеет единственный корень, который находится подбором. Получаем х = 1.
Ответ: х = 1.
4. Пусть одно из чисел равно х, тогда второе равно 48 – х. Найдем сумму куба первого числа и квадрата второго числа и получим функцию f(x) = х3 + (48 – х)2. Найдем ее производную: /
Стационарные точки функции 
или x1 = -6 и х2 = 16/3. Отметим эти точки на координатной оси и нарисуем диаграмму знаков производной. Видно, что функция имеет минимум при х = 16/3. Тогда второе число 48 – x = 128/3. Эти два числа положительные, что соответствует условию задачи.
Заметим, что если числа поменять местами, то по аналогии будем иметь функцию f(х) = (48 – х)3 + x2. Производная этой функции 
Видно, что функция f(x) убывает при всех х и наименьшего значения не имеет.
Ответ: 16/3 и 128/3.
5. Легко сообразить, что с > 0. Пусть касание происходит в точке а. Найдем f(x) = 2сх и напишем уравнение касательной: у = 2са(х – а) + са2 или у = 2сах – са2.
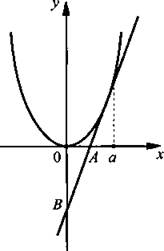
Найдем координаты точек пересечения касательной с осями координат. При х = 0 имеем: у = -са2 и ОВ = са2. При у = 0 получаем уравнение 0 = 2сах – са2, откуда х = a/2 и OA = a/2. Тогда 
