Цели: сообщить результаты работы; рассмотреть типичные ошибки; разобрать трудные задачи.
Ход урока
I. Сообщение темы и целей урока
II. Итоги контрольной работы
III. Ответы и решения
Вариант 1
2. а) Функция четная; б) π/2.
3. а) Функция возрастающая; б) график симметричен относительно оси абсцисс.
Вариант 2
2. а) Функция нечетная; б) 2π/3.
3. а) Функция убывающая; б) график симметричен относительно оси абсцисс.
Вариант 3
1. Нечетная.
2. 
3. 2π.
4. ymin = 4, ymах = -4.
5. а) График симметричен относительно оси ординат; б) семейство прямых 
Вариант 4
1. Четная.
2. 
3. 2π.
4. ymin = 6, ymах = -6.
5. а) График симметричен относительно оси ординат; б) семейство прямых 
Вариант 5
1. Найдем 
Было учтено, что функция косинуса четная и 
Так как у(-х) = -у(х), то функция у(х) нечетная по определению.
Ответ: нечетная.
2. Область определения задается условием, что функции tg 2x и ctg 2x определены. Поэтому 
Функция у(х) нечетная. Для tg 2х > 0 и ctg 2х > 0 запишем неравенство между средним арифметическим и средним геометрическим: 
Таким образом, D(y) – все x,кроме 
и 
Ответ: D(y) – все х, кроме 
3. Найдем периоды функций, входящих в функцию y(x). Получим: для функции 
для функции 
для функции 
НОК 
Поэтому период функции y(x) равен Т = 2π.
Ответ: 2π.
4. Запишем данную функцию в виде 
Обозначим 
и получим: 
Наименьшее значение функции достигается при t = -1/3 и равно 
наибольшее значение достигается при t = 1 и равно 
Ответ: 
5, а. Для данной функции раскроем знак модуля и получим: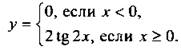 
Построим график этой функции. Учтем, что график функции у = 2 tg 2x получается из графика у = tg х растяжением в два раза вдоль оси ординат и сжатием в два раза вдоль оси абсцисс.
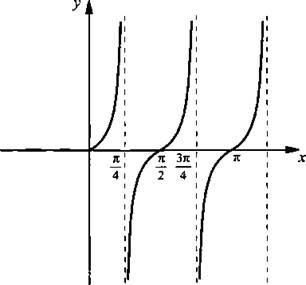
Ответ: см. график.
5, б. Выпишем решения уравнения 
и получим: 
При n = 0 получим: x = у = 0 (начало координат), при n = 1 имеем график уравнения 
при n = 2 получим график уравнения 
Строим графики таких уравнений. Графиком данного уравнения являются точка, находящаяся в начале координат, и вложенные друг в друга ромбы, стороны которых отличаются в два раза.
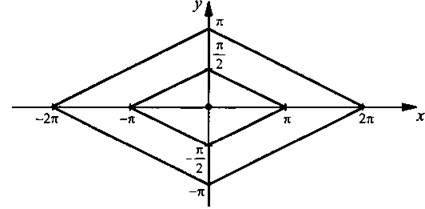
Ответ: см. график.
Вариант 6
1. Найдем 
Было учтено, что функция котангенса нечетная и |-x| = |х|. Так как у(-x) = -у(х), то функция y(x) нечетная по определению.
Ответ: нечетная.
2. Область определения задается условием, что функции tg 3х и ctg 3x определены. Поэтому 
Функция y(x) нечетная. Для tg 3х > 0 и ctg 3х > 0 запишем неравенство между средним арифметическим и средним геометрическим: 
Тогда 
Таким образом, D(y) – все х, кроме 
и 
Ответ: D(y) – все х, кроме 
3. Найдем периоды функций, входящих в функцию y(х). Получим: для функции ctg 3х –
для функции cos х – 
для функции sin 2х – 
НОК 
Поэтому период функции у(х) равен Т = 2π.
Ответ: 2π.
4. Запишем данную функцию в виде 
Обозначим t = cos x (где -1 ≤ t ≤ 1) и получим: у = -2t2 + 3t +1. Наибольшее значение функции достигается при t = 3/4 и равно 
наименьшее значение достигается при t = -1 и равно yнаим = -2 – 3 + 1 = -4.
Ответ: 
5. а. Для данной функции раскроем знак модуля и получим: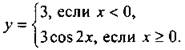 
Построим график этой функции. Учтем, что график функции у = 3 cos 2х получается из графика у = cos х растяжением в три раза вдоль оси ординат и сжатием в два раза вдоль оси абсцисс.
