Цели: сообщить результаты работы; рассмотреть типичные ошибки; разобрать трудные задачи.
Ход урока
I. Сообщение темы и целей урока
II. Итоги контрольной работы
1. Распределение работ по вариантам и результаты решения. Данные о результатах работы удобно заносить в таблицу (для каждой пары вариантов).
|
№ задачи Итоги |
1 |
2 |
3 |
… |
6 |
|
+ |
5 |
|
|
|
|
|
± |
1 |
|
|
|
|
|
– |
1 |
|
|
|
|
|
∅ |
1 |
|
|
|
|
Обозначения:
+ – число решивших задачу правильно или почти правильно;
± – число решивших задачу со значительными ошибками;
– – число не решивших задачу;
∅ – число не решавших задачу. Вариант 1, 2-8 учеников.
2. Типичные ошибки, возникшие при решении задач.
3. Наиболее трудные задачи и их разбор (учителем или школьниками, решившими эту задачу).
4. Разбор всей контрольной работы (вывесить на стенде ответы к заданиям вариантов и разобрать наиболее трудные варианты).
III. Ответы и решения
Вариант 1
1. Возрастает на промежутке [2; +∞) и убывает на промежутке (-∞; 2], унаим = у(2) = -9.
2. Функция нечетная.
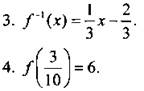
5. а, б построены.
Вариант 2
1. Возрастает на промежутке (-∞; -3] и убывает на промежутке [-3; +∞), унаиб = у(-3) = 16.
2. Функция четная.
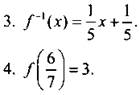
5. а, б построены.
Вариант 3
1. Возрастает на промежутке [0; +∞) и убывает на промежутке (-∞; 0], унаим = y(0) = 6.
2. Функция четная.
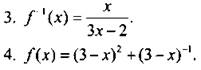
5. а, б построены.
Вариант 4
1. Возрастает на промежутке (-∞; 0] и убывает на промежутке [0; +∞), унаиб = у(0) = -12.
2. Функция нечетная.
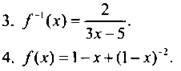
5. а, б построены.
Вариант 5
1. Запишем данную функцию в виде ![]() Дробь
Дробь ![]() с ростом |x| убывает. Поэтому функция у(х) возрастает на промежутке (-∞; 0] и убывает на промежутке [0; +∞). Наибольшее значение функции унаиб = у(0) = 3.
с ростом |x| убывает. Поэтому функция у(х) возрастает на промежутке (-∞; 0] и убывает на промежутке [0; +∞). Наибольшее значение функции унаиб = у(0) = 3.
Ответ: возрастает на промежутке (-∞; 0] и убывает на промежутке [0; +∞), унаиб = у(0) = 3.
2. Область определения функции (-∞; +∞). Найдем: ![]()
![]() Так как выполнено равенство у(-х) = -у(х), то данная функция нечетная.
Так как выполнено равенство у(-х) = -у(х), то данная функция нечетная.
Ответ: функция нечетная.
3. Из равенства ![]() выразим х:
выразим х: ![]() тогда
тогда ![]() Введем переобозначения х ↔ у и найдём обратную функцию:
Введем переобозначения х ↔ у и найдём обратную функцию: ![]()
Ответ: ![]()
4. Запишем функцию в виде ![]() Найдем:
Найдем: ![]() Тогда
Тогда ![]()
Ответ: ![]()
5, а. Построим в одной системе координат графики функций y1 = x + 2 и у2 = х2 (пунктирные линии). Они пересекаются в точках (-1; 1) и (2; 4). При каждом значении х из значений функций у1 и у2 выбираем наименьшее значение. Получаем график данной функции (сплошная линия).
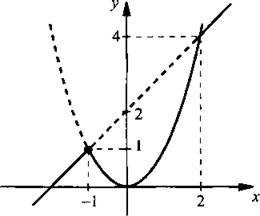
Ответ: график построен.
5, б. Разложим числитель дроби на множители и сократим ее. Получаем: ![]() Таким образом, надо построить график функции у = (х + 4)(х + 2) (парабола) при условии х + 1 ≠ 0, т. е. х ≠ -1.
Таким образом, надо построить график функции у = (х + 4)(х + 2) (парабола) при условии х + 1 ≠ 0, т. е. х ≠ -1.
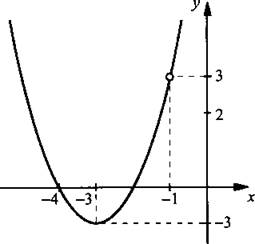
Ответ: график построен.
Вариант 6
1. Запишем данную функцию в виде ![]() Дробь
Дробь ![]() с ростом |x|убывает. Поэтому функция y(х) возрастает на промежутке [0; +∞) и убывает на промежутке (-∞; 0]. Наименьшее значение функции yнаим = y(0) = -4.
с ростом |x|убывает. Поэтому функция y(х) возрастает на промежутке [0; +∞) и убывает на промежутке (-∞; 0]. Наименьшее значение функции yнаим = y(0) = -4.
Ответ: возрастает на промежутке [0; +∞) и убывает на промежутке (-∞; 0], yнаим =y(0) = -4.
2. Область определения функции 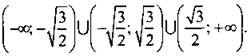 Найдем:
Найдем: ![]()
![]() Так как выполнено равенство у(-х) = у(х), то данная функция четная.
Так как выполнено равенство у(-х) = у(х), то данная функция четная.
Ответ: функция четная.
3. Из равенства ![]() выразим x:
выразим x: ![]() тогда
тогда 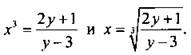 Введем переобозначения х ↔ у и найдем обратную функцию:
Введем переобозначения х ↔ у и найдем обратную функцию: 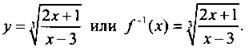
Ответ: 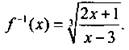
4. Запишем функцию в виде ![]() Найдем:
Найдем: ![]() Тогда
Тогда ![]()
![]()
Ответ: ![]()
5, а. Построим в одной системе координат графики функций y1 = -х – 2 и у2 = -х2 (пунктирные линии). Они пересекаются в точках (-1; -1) и (2; -4). При каждом значении х из значений функций у1 и у2 выбираем наибольшее значение. Получим график данной функции (сплошная линия).
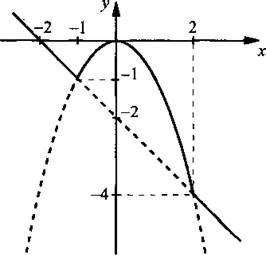
Ответ: график построен.
5, б. Разложим числитель дроби на множители и сократим ее. Получим: ![]() Таким образом, надо построить график функции у = (х – 3)(х – 5) (парабола) при условии х – 2 ≠ 0, т. е. х ≠ 2.
Таким образом, надо построить график функции у = (х – 3)(х – 5) (парабола) при условии х – 2 ≠ 0, т. е. х ≠ 2.
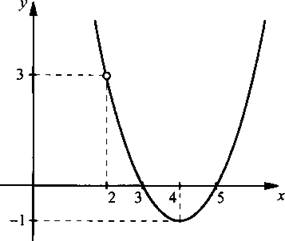
<sp














